Transcription of Multa et mira de Angulo contactus (13 Dezember 1681)
Multa et mira de Angulo contactus notavi in scheda, 1 Xb. cujus inscriptio est: Lineae datae parallelam ducere per punctum datum.

Res eo redit, ut angulus consideretur, quem facit una tangens ad vicinam, sint duae curvae $ABC.$ $DEC.$ tangens utrique communis $CT$ axi $MT$ occurrens in $T$ tangunt enim se curvae in puncto $C$.

Ponantur puncta $E$ et $B$ etiam coincidere et rectam $BC$ sumi pro latere polygoni infinitanguli curvam repraesentantis. Sumatur ejusdem polygoni curvae $ABC$ aliud punctum $A$, et curvae $DEC$ punctum $D$. Jungantur chordae $AB$, $DE$ sive $AB$. $DB$ posito $B$ et $E$ coincidere et $BA$ producatur dum axi occurrat in $F$, et $ED$ axi occurrat in $G$. Tunc angulus contactus curvae $DEC$ ad rectam tangentem communem major est, si angulus $GET$ sit major quam $FBT$.
Unde patet angulos contactus crescere cum infinite parvis, sunt enim $TF$. $TG$ infinite parvae; subtensae nempe angulorum $FBT.$ $GBT.$ infinite parvorum.
Verum mensuram anguli contactus hinc petere non licet prout enim $DE$ sumitur major aut minor, alia oritur quantitas anguli, aliaque rectarum $TG,$ $TF$ ratio inter se invicem vel etiam arcuum quibus hi anguli insistunt. Nec refert etsi $DE.$ $BC$ semper sumantur aequales; Possunt enim esse semper aequales, et tamen dimidio minores.
Solus circulus hoc habet, ut ubique eundem habeat angulum contactus ad eandem rectam, itemque angulum contactus ab utraque parte aequalem. Idem est si plures Circuli se tangant.
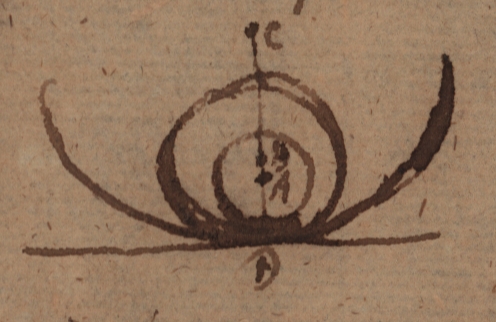
Est quoque anguli contactus quantitas idem cum lineae curvedine. Circulorum autem curvedines sunt in ratione radiorum generantium $AD.$ $BC.$ $CD$; quia omnes circuli sunt similes et curvedines eorum similiter producuntur, sunt ergo effectus in ratione causarum. Neque enim discerni possunt nisi compraesentia, vel adhibito aliquo tertio nempe recta vel alio dissimili ad ipsos aut dissimiliter posito.

Jam caeterarum omnium curvarum curvedines possunt aestimari a circulis inscriptibilibus. Sit curva $GDE$ cui inscriptilis est circulus radio $AD$ descriptus tangens in puncto $D$. Is scilicet in parte curvae concava totus poni potest seu totus jacet intra curvam. In eadem recta ad curvam perpendiculari $DA$, quantum satis producta, sumatur punctum $C$ tale ut centro $C$ radio $CD$ descriptus circulus (qui curvam tanget in $D$, quia $CD$ est ad curvam perpendicularis) curvam iterum alicubi secet in $F$. Is itaque circulus cujus radius $CD$ utique curvae non est ita inscriptilis, ut eam tangat in puncto $D$. Quaeritur circulus inscriptilium in puncto $D$ tangentium maximus, cujus centrum sit punctum $B$. Hujus igitur radii $BD$ magnitudo quantitatem curvedinis determinabit. Calculo autem investigari potest, quia circulus centrum habens in recta $DC$ eo ipso quia curvam $GDE$ tangit, facit aequationem duas habentem radices aequales. Sed hoc modo si punctum $F$ incidat in punctum $D$ < - - - fiunt> minimum tres radices aequales.
Ergo ut tangentes sive directiones curvarum investigantur per rectas tangentes et duas radices aequales, ita anguli contactuum, sive directionum mutationes sive curvedines investigantur per circulos tangentes, et tres radices aequales. Habemus ergo problema quod tot ingenia exercuit absolutum tandem, et reductum ad puram Geometriam. Angulus communis exprimitur maginitudine arcus; angulus contactus seu curvedo magnitudine circuli, seu radii. Ille magnitudine curvae, hic rectae. Recta utrobique extra curvam ad convexitatem tendens est tangens curvae seu exprimit curvae directionem. Circulus tangens intra curvam seu ad concavitatem ad alteram partem tendentium circulorum tangentium maximus, exprimit curvae in illo puncto curvedinem ad illam partem seu contingentiae quantitatem.
Considerandum in genere, data curva, in quot punctis ei occurrere possit circulus ad summum; unde jam ista erunt aestimanda. Curvarum praeter circulum (et helicem cylindricam ex illis quae in plano describi non possunt) curvedo ubique mutatur. Potest tamen exhiberi ejus maxima et minima curvedo. Hinc potest circulus $AD$ tam esse parvus, ut perpetuo intra curvam $ADE$ procedere et rotari possit ita ut nunquam in ipsam illidatur. Potest etiam circulus $CD$ tam esse magnus, ut nunquam intra curvam rotari possit. Circulus maximus qui intra curvam totam rotari potest, est is cujus curvedo est eadem cum maxima curvae curvedine. Et cum hunc quaeremus, credo quatuor ad minimum radicibus aequalibus opus fore. Nimirum maxima curvedo habebit curvedines ab utraque parte decrescentes caeterae habebunt ab una parte crescentes ab altera decrescentes. Itaque ut tangens forte adhuc alibi occurrere potest, ita potest esse maxima media curvedo pro parte curvae, (nam maximam extremam habet quaelibet pars. Maximam mediam voco quae radii habet decrescentes, ab utraque parte) et circulus qui eandem curvedinem habet per maximam determinabitur.
Cum autem dicitur curvedinem curvae eandem esse in aliquo puncto, quae est alicujus circuli tunc intelligendum est curvedinem in eodem puncto ab una tantum parte. Nam ut circa idem punctum duo sunt anguli contactus, qui possunt esse valde inaequales, et solent quoque esse in curvis excepto circulo et helice cylindrica; ita quoque duplex est curvedo: igitur cum dicitur tantam esse curvedinem, in puncto aliquo, dicendum est ad quas partes.

Ita ponamus circulum $AD$ rotando venientem ab $E$ versus $D$. Ubi illidi intra curvam nec posse amplius rotando progredi ita ut omnia ejus puncta successive ordine tangat (nam per saltum porro progredi posset) multa puncta transmittendo inter $D$ et $H$. quae duo scilicet puncta tunc simul tangit. Relictis intermediis arcus $DH$. Verum puto ad hoc impedimentum progressus non esse attendendum quia per accidens fit, ut posita tam magna $DH$ sed debet esse impedimentum in ipsa $DH$ utcunque exigua a $D$ versus $H$ continuata itaque potius considerandum an circulus post contactum egrediatur e curva ita ut postea iterum eam secet ut in pagina praecedenti designavimus. Est autem $DF$ pars circuli centro $D$ descripti necessario intra curvam, quia circulus curvam tangit a parte concava. Jam si quaeratur radius $BD$ talis ut punctum $F$ incidere incipiat in $D$ tunc $BD$ exprimit magnitudinem curvedinis. Sed alius poterit esse circulus quo idem fiet a parte altera $DE$. Interdum tamen angulus contactus seu curvedo ab utraque parte eadem cum scilicet constat utrobique eodem modo ad tangentem referri ut tangens verticis parabolae Hyperbolae vel Ellipsis, seu tangens ad axem perpendicularis, facit angulum contactus utrobique aequalem.
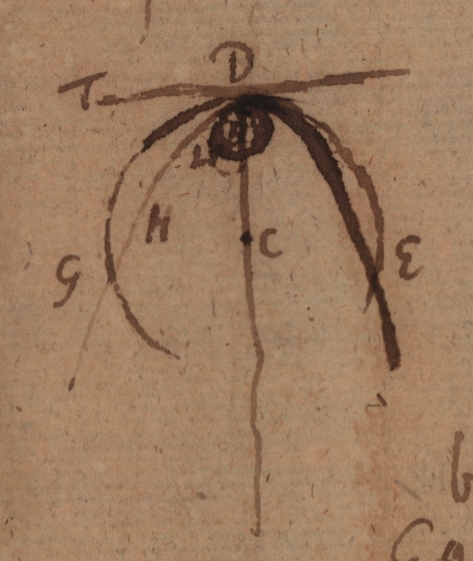
Jam melius video sit parabola $GDE$, cujus vertex $D$. perpendicularis ad curvam seu ejus tangentem, in vertice est ipse axis $CD$. Sumto jam alicubi puncto in Axe $C$. radio $CD$ descriptus circulus utique curvam tanget. Sed is si cadat extra curvam iterum eam secabit et quidem in duobus punctis utrobique eodem modo. Habet ergo duas radices aequales quatenus tangit in $D$. Item oppositas aequales ob $G$ et $E$. Sed si $CD$ sit tam parva ut $G$ et $E$ incidant in $D$, tunc coincident omnia quatuor puncta, in quibus circulus parabolae occurrit. Et ejus circuli radius sit $DB$, inscriptilium maximus. Equidem patet non coincidere duas curvas circuli $BD$ et parabolae, ideoque angulum contactus parabolae ad $TD$ tangentem esse minorem quidem, quam circuli $BD$ ad eandem tangentem, sed dicendum est differentiam esse infinite parvam respectu ipsius anguli contactus; adeoque cum ipse angulus contactus $HDT$ sit infinite parvus respectu rectilinei erit angulus contactus $LDH$ infinite parvus respectu ipsius $HDT$ atque adeo infinities infinite parvus respectu rectilinei. Hinc uti angulus rectilineus est major quolibet angulo contactus ita angulus contactus circularis major quolibet angulo contactus curvae ad circulum suae curvedinis quia ut tangens recta directionem curvae, ita tangens circulus inscriptilium maximus curvedinem exprimit. Differentiae habentur infinite parvae. Hoc $\langle$-$\rangle$ non intellecto nemo se expediet.
[In the margin NB. solutio summae difficultatis

Ne quis autem putet eo casu quo puncta $D.$ $G.$ $E$ coincidunt, fieri radium $BD$ etiam infinite parvum; dabo exemplum ubi manifestum est contrarium. Sit curva $EDG$ quam a circulo ex centro $B$ radio $BD$ descripto intus tangi certa est (utique enim talis curva vel ejus portio datur). Trans ea sumatur praeterea punctum aliquod $L$ et angulo $LDB$ sit aequalis $FDB$, et rectae $GD.$ $ FD.$ aequales, habebitur punctum $F$ et per tria puncta $LDF$ describatur circulus centro utique $C$ in axe existente, quia duo puncta $L.$ $ F.$ aequidistantia a $D$ etiam se eodem modo ad axem habent is circulus ergo $LDF$ curvam tanget in $D$. Sed idem extra eam egredietur et secabit eam in puncto aliquo $G$, ponatur jam hic circulus continue diminui donec punctum $G$ incidere incipiat in punctum $D$. Utique is circulus erit quem quaerimus cujus scilicet curvedo eadem quae curvae datae. Idem patet sic quoque. Diminuatur circulus $CD$ centro continue accedente versus $B$. Ergo cum in $B$ venerit, cadet totus intra curvam, ergo vel paulo major jam intra eam cecidit, et designari poterit punctum inter $C$ et $B$ quo intra eum cadere incepit vel primum incipit in $B$. et tunc $B$ erit centrum circuli quaesiti.
Si jam curva $GDE$ eodem modo se habet ab utraque parte ad rectam $DC$ seu si est axis tunc angulus contactus utrobique idem. Sed si sit diversus ut si sit radius $BD$ maximus intus tangentium curvam $GD$ seu quo $G$ incidit in $D$. at non ideo $F$ incidat in $D$. sed circuli ex $BD$ sinistra medietas. Statim ingrediatur citra curvam $GHD$. Dextra vero medietas curva $DE$ egrediatur, patet diversas esse curvedines, ut circulus $BD$ habebit curvedinem curvae $GHD$, versus $H$. at circulus major $CD$ maximus ingredient$\langle$ium$\rangle$ intra $DE$ versus $F$ exgrediatur ex $DH$ versus $L$. Is exprimet curvedinem curvae in puncto $D$ versus $E$. Idem patet etiam ex punctis flexuum.
Puncta flexuum habentur per coincidentiam trium punctorum, in quibus recta talem curvam secat. Curvedines habentur per coincidentiam trium punctorum in quibus circulus curvam ab ea parte ad quam curvedo esse intelligitur, secat. Curvedinem coincidere cum angulo contactus ex eo patet quod curvedo utique est directionum ad se invicem inclinatio sive directionum per minima mutatio, id vero est quoque angulus curvae ad tangentem seu angulus tangentis ad tangentem proximam. Quia sumendus angulus contactus in puncto quantum satis vicino, unde chorda ad punctum contactus ducitur chorda autem in puncto indefinite vicino est ipsa tangens.
Post tractatas directiones seu tangentes tractandae sunt quoque curvedines seu directionum mutationes seu anguli contactuum.
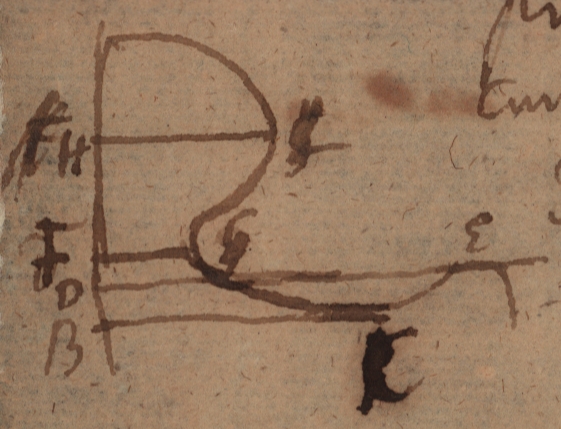
Videndum an curvae duae inaequales possint habere easdem curvedines, seu an curvae parallelae easdem habeant curvedines, an vero aliae puncta reversionum determinant maximam et minimam curvae ordinatam. Punctum reversionis moti regulae per directricem exhibet reascensum vel redescensum respectu condirectionis curvae, seu ordinatam quae est tangens ut $BC.$ $DE.$ sed punctum reversionis mobilis in regula dextrorsum vel sinistrorsum, seu appropinquatione vel respectu directricis, exhibet ordinatam maximam vel minimam perpendicularem $FG$. vel $HL$.
Notandum in puncto flexus quodammodo curvam habere duas diversas tangentes et nullam; an forte tunc punctum curvae quiescit atque ita nulla tunc ejus directio est?


Aliquando infiniti curvae tangentes dari possunt ad unum idem punctum; sit curva mota hoc modo: $ABCDEBFGHLFM$ patet infinitas esse tangentes exiguae particulae $BCDE$ utcunque illa contrahatur, adeo, ut etsi tandem fiat infinite parva, tamen maneant infiniti tangentes, ut in connexione $B$ duarum semicycloidum $AB.$ $BF.$ Hoc si accommodetur ad modum nostrum generalem describendi curvas, patebit illic fieri reversiones sursum deorsum dextrorsum sinistrorsum, et infinitas interim directionum mutationes tempore infinite parvo, per spatia infinite parva; si tangens realis semper cum puncto circumferetur, directionem curvae exprimens, ea deberet momento absolvere totum circulum seu unam circulationem. Hinc contingunt infinitae directiones simul. Videntur hoc casu esse duae curvae.
Per reversiones patet dari duas radices aequales, ut ita nullo respectu habito ad tangentes. Patet enim ibi duas ordinatas in unam coalescere.
Modus describendi curvam per focos, vel adhibitis meris regulis cum funibus, vel curvis vel etiam curvis et regulis cum funibus, et curvis vel constanti[bu]s longitudinibus si per extremorum foramen transeat funis vel curvis evolutis, extremo funiculi ad curvam existente libero.
