Ars Combinatoria
This section contains as yet unpublished manuscripts by Leibniz that concern the Ars Combinatoria and more particularly his tabular methods. The German philosopher's combinatorial practice is based on two tools: the table, which Leibniz links to inventories, and thus to the Ars Inveniendi, and the form, which he links to the characteristic, and thus to the Ars Characteristica. The table and the form are in fact two sides of the same coin: one develops and the other envelops. Indeed, the table is a tool that allows Leibniz to arrange different terms in bidimensional space. The relations between these terms then establish a synoptic panorama of the different possible combinations and the way they are generated. The form, on the other hand, envelops all the combinations within it. The combinatorial structure is expressed by means of the identical. Indeed, the equality between two forms expresses the invariants that define the combinatorial subclasses of a structure.
It is through the tabular practice that combinatorics is first integrated within Leibnizian mathematics, at the beginning of the Parisian stay. These works, published in the third volume of the Akademie's series VII, deal with questions of series and quadratures. From 1674 onwards, Leibniz worked intensively on algebraic questions and the tables gradually took on a purely heuristic role in his work.
The texts we propose here are texts from after the Paris period (1677-1680), in which Leibniz uses tables to analyse problems related to series and quadratures, despite his considerable interest in formal aspects and symbolic problems at that time. These texts constitute a double counterweight in the image that one tends to construct of Leibniz's mathematical practice. On the one hand, Leibniz uses diagrams as a tool for calculation and not only as a support for the imagination, which should be distrusted. On the other hand, he is an experimental mathematician who gives great importance to induction and does not resign himself to reducing all reasoning to a mechanical and deductive derivation.
De summis serierum Arithmo-Geometricarum infinitarum
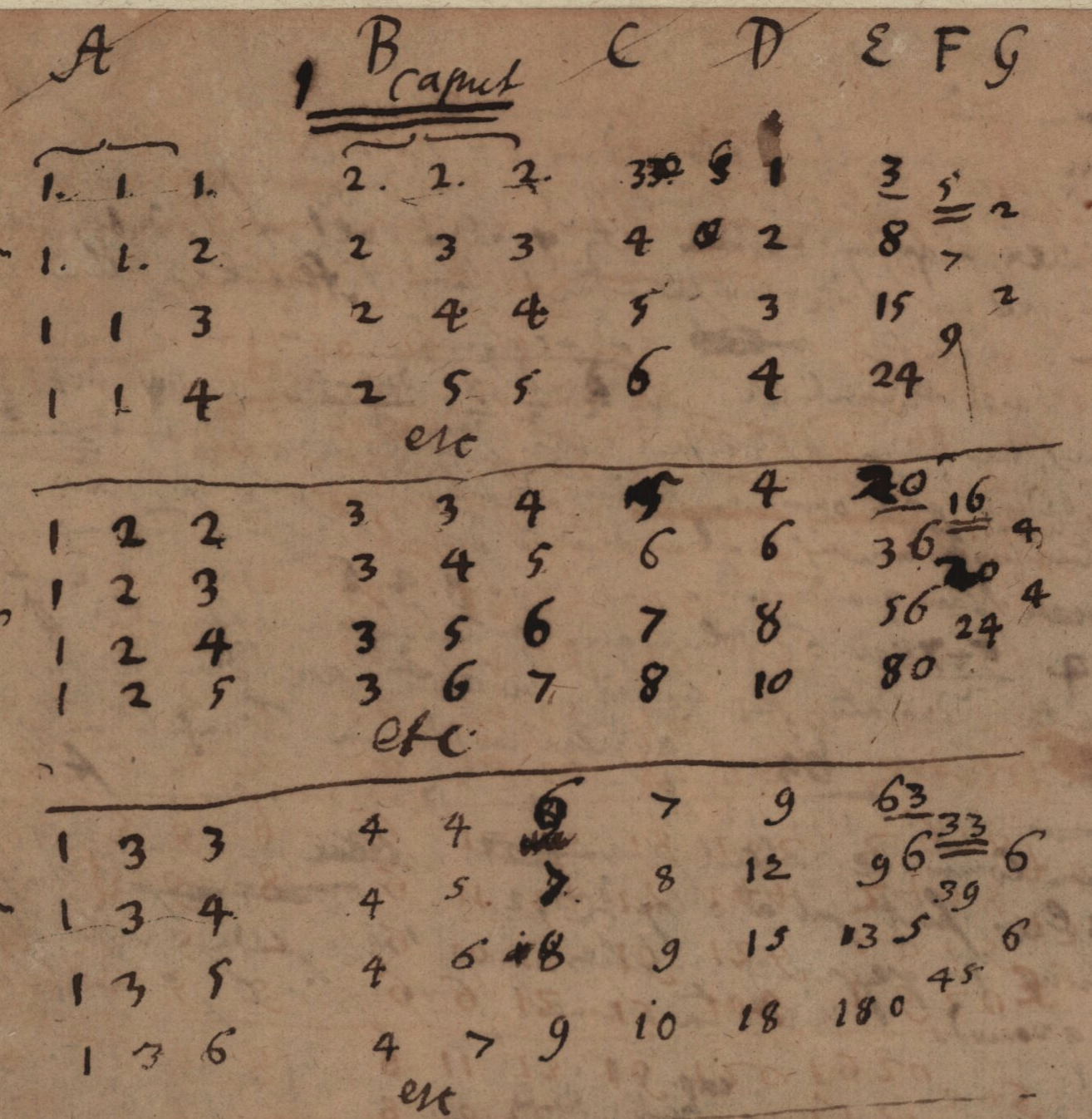
Overview of De summis serierum Arithmo-Geometricarum infinitarum
Leibniz wrote this text in January 1678, i.e. a period shortly after his departure from Paris when questions about the analysis of progressions were gaining in interest. The problem Leibniz wanted to solve was to find the sum of what he called arithmo-geometric series: $0^p.t + 1^p.t^2 + 2^p.t^3 + \dots + (n-1)^p.t^n + \dots$ The terms of the series are composed of two factors, one of which, $t^n$, follows a law of geometric progression, and the other $n^p$ follows an arithmetic law, raised to a certain power $p$.
This text has many interests, starting with that of underlining the very important role played by the difference triangles that Leibniz developed at the beginning of his stay in Paris. Indeed, at first sight this text deals with quadrature problems, which the introductory diagram seems to confirm. The presence of numerous equations suggests the use of algebra to solve geometric problems, which is not original. But the framework that Leibniz chooses to deal with the question is actually much closer to the combinatorial framework in which Leibniz develops difference triangles. The diagrammatic aspect of these triangles is subsumed in the reasoning and leads the philosopher to the construction of another table, equally combinatorial.
Leibniz even announces the opposite, namely that the method of differences is only a special case of the method he presents here ("Finding the series by means of differences is only a specific case of this method"). But the technique of decomposition is the same, and so one can also see this particular case as a canonical example that serves as a model.
Indeed, Leibniz calculates the difference between the given series $X$ and the series obtained by shifting the series by one term $Y$, to find series that are of a lower degree $p$. The process is a recursive one, i.e. these series can in turn be decomposed into series of lower degree up to the degree $p=0$ where the series is necessarily the following geometric series: $t + t^2 + t^3 + \dots + t^n + \dots = \frac{t}{1-t}$ Leibniz calls this series $S$. But the series $X$ is in fact the product of the given series $Y$ by the variable $t$. So $Y-X = \frac{1}{t}X-X= \frac{1-t}{t}X = \frac{X}{S}$. Therefore $X = S\times (Y-X)$. Thus, Leibniz progressively decomposes all series into sums and products of the $S$-series, hence a polynomial in $S$.
In this double equation, Leibniz realises that the $Y$ series is eliminated without even calculating it ("the technique consists in this of supposing mean terms and new unknowns"). The underlying philosophical reflection here concerns the form of deductive reasoning. Here, pure analysis is not enough. An element external to the problem must be attached for the deduction to be able to start. If it were necessary to obtain a complete resolution of this added element, it would then constitute a part of the problem and its study would represent a stage of the analysis. But the fact that we do not need to determine this addition completely confirms that this object is external to the problem, and that this reasoning contains a part of synthesis, or in other words, of combinatorics.
Untitled (Tables sur la formule de Heron)
Overview of Untitled (Tables sur la formule de Heron)
This manuscript is dated March 1678. It is part of a corpus of texts in which Leibniz works on diophantine problems, in particular triangles in numbers, i.e. triangles whose sides all have integer ratios to each other. Here, Leibniz thus engages in a systematic study of this problem, developing a method for generating all possible triangles in numbers. However, isolating this manuscript from the arithmetical context in which it appears to be set, Leibniz's presentation of it places it more within the framework of geometry, and more particularly geodesy. In mentioning this discipline, Leibniz refers directly to Heron of Alexandria, whose famous formula for determining the area of any triangle from its three sides is being studied. Thus, this manuscript must be situated at the crossroads of research on practical mathematics and applied geometry and those interested in number theoretical problems.
The mathematical aspects of this text are very valuable, because here Leibniz pushes the method of finite differences to a level of complexity that is not found elsewhere. As a reminder, at the beginning of his stay in Paris, Leibniz developed a method for analysing progression by successive differences in the form of a
numerical table: the difference triangle. At first he saw this as a real field of theoretical research, but he quickly turned away from this position. Thus, the difference triangles quickly became an essential heuristic tool for the young philosopher, but at the same time they acquired a standard, very stable form, no longer being themselves the object of questioning but a tool for answer. This text therefore shows an extremely original practice of the triangle of differences, which has no equivalent in the corpus as far as we know, and which is extremely late, since in 1678 the practice had been stabilised for more than three years.
This text thus testifies to the fact that tabular practice retains a central place in the Leibnizian method. And despite an apparent local stabilisation of certain practices, the philosopher continues to see it as a tool that can be further developed for the progress of the art of inventing.
More concretely, after a change of variables produced by purely combinatorial reasoning, Leibniz makes a complete list of the triplets of numbers that can produce a triangle. This list depends on three parameters which are the three differences. Therefore, by listing all the areas of all the triangles, Leibniz does not obtain a classical unidimensional progression, but a quantity that progresses in three directions. Thus, the method of difference triangles, based on the relation between a term and its neighbour, no longer operates, since a term has several neighbours. Leibniz therefore develops here a three-dimensional difference triangle, which establishes the differences of terms in three steps. First the triangle table gives the difference triangles for the variable f. Then the table of members gives the triangles for the variable e and finally the table of heads gives those for the variable d. Each step uses the previous step. The
Leibniz procedure is not commutative and gives asymmetric roles to the three variables. It is therefore more accurate to say that this table has several layers than to say that it has several dimensions. Indeed, the differences are always made in a fixed order and Leibniz does not mention the fact that one can
obtain the same values by following other paths. For this reason, it would be unreasonable to see in this procedure a discrete version of partial derivatives.
Nevertheless, the values obtained in the head table do correspond to the coefficients of the partial derivatives of Heron's formula (taken with Leibniz's parameterization). Moreover, it is clear that this text shows a differential method to analyse quantities that depend on several parameters.
Finally, we add to this manuscript a fragment that is obviously related to it. The short paragraph of text in this fragment confirms Leibniz' position on the use of difference triangles. The aim is to obtain coefficients that reduce the calculation of areas to a simple sequence of addition and subtraction, in order to relieve the
mind of any calculation.
Tabula Numerorum Arithmeticae Replicationis seu Figuratorum interpolata
Overview of Tabula Numerorum Arithmeticae Replicationis seu Figuratorum interpolata
This manuscript is a copy of the interpolation table found in Wallis' Arithmetica Infinitorum of 1656, at
proposition 135, p.165.
The precise dating of this manuscript is difficult, as it is undated and contains almost no references or mentions that could serve as a solid terminus a quo. There are three groups of manuscripts with which it can be associated. In the first, dated 1679, Leibniz explores the interpolation techniques of Pietro Mengoli and refers to the work of Wallis. The second, dated 1686, is concerned with formalising the Wallisian quadratures in the context of differential calculus. Finally, the third group is undated, but must be later than 1693, as they are working notes on a collection of Wallis' texts published that year. The writing and use of symbols makes this manuscript more like the 1686 and post-1693 groups than the first group of 1679. Nevertheless, the fundamental question of the expression of transcendental quantities is present in all three groups, which testifies to the non-linear character of Leibniz's thought, which weakens any dating hypothesis based solely on a genetic reconstruction of a reasoning.
This text presents two major interests. The first is the complete copy of the interpolation table. Leibniz does not leave out any terms in the table, which suggests that it is not only a matter of thinking during the concrete process of constructing the diagram but also of thinking from the completed diagram. Leibniz's main work on questions of interpolation can be found in Parisian texts or in the 1679 group. In all these texts, the interpolation tables are based on the work of Pietro Mengoli and not on Wallis. This is therefore the only Wallisian version of an interpolation table in Leibniz that we know of.
Given the difficulty of dating this manuscript, putting its contents into context is perilous. Indeed, such a work does not have the same significance if it dates from the late 1690s, when Leibniz started a correspondence with Wallis himself, or if it dates from the mid-1685s, before the trip to Italy, the writing of the Dynamica and the turning point of the 1690s with regard to Leibniz's conception of the ars Combinatoria and the Mathesis Universalis. Therefore, it is appropriate to focus on the content of the text only.
The second interest of this text lies in the fact that Leibniz confronts in it two mathematical approaches that are fundamental in his work: the formal approach and the tabular approach. When he sets out to generalise the quadrature formula from Wallis' work by a method inspired by Newton's binomial development, namely to find a formula that is infinite when the exponent is not integer, but finite when it is, Leibniz realises that he obtains different values from those obtained by Wallis' inductive interpolation process. Thus, the two approaches are not equivalent.
Nevertheless, Leibniz does not see this as a sign that the two approaches are incompatible, but rather that the solution to generalise the formula is not yet satisfactory. Leibniz's goal of achieving a correspondence between the formal properties of equations and the algorithmic processes on diagrams is particularly well illustrated in this text. Furthermore, this analysis could serve as a basis for comments on the place of harmony in the German philosopher's work.
Untitled, sur l’interpolation de Mengoli
Overview of Untitled, sur l’interpolation de Mengoli
This text is part of a wider investigation by Leibniz in 1679 into the question of transcendence. On this occasion, he reopened a file that he had probably closed at the end of his stay in Paris in 1676: the interpolation techniques of Wallis and Mengoli for squaring the circle.
On the front are two triangular diagrams derived from Mengoli's triangular tables, which are probably copies of the diagrams that Leibniz wrote in his 1676 notes on Mengoli's Circolo. In the left-hand margin of the triangular tables, there is a geometric description of the curves represented by each term of the triangle. In the right-hand margin, Leibniz compares the advantages of this tabular method with those of Newton's formula.
This first part is devoted to the search for a method of determining a transcendental expression for squaring the circle, based on the tabular method of Mengoli and Wallis. Leibniz notes that one of the terms of the triangle must be expressed differently, depending on whether it is considered to be the term of a diagonal or horizontal sequence in the table. For him, this can be explained by the fact that the common denominator of all the terms of the table is transcendental. This search for a transcendental expression for quadratic curves such as the circle must therefore involve thinking about exponents. Therefore, Leibniz thinks that he can express the circle with a transcendental but finite expression.
Overleaf, Leibniz emphasises the role of differential calculus in these quadratic problems. The relationship between the two linked variable abscissas and residue can be of two kinds: $r+a$ is a constant or $r-a$ is a constant. In the first case, the quadratures depend on that of the circle, while in the other they depend on that of the hyperbola. Leibniz wants to know how these two very similar types of relationship could be articulated: on the one hand, the relationships induced by the triangular tables of Mengoli or Wallis and, on the other, those deduced by the differential algorithm.
Finally, a marginal paragraph describes a geometric figure that represents the relationships obtained by applying the differential algorithm. The diagram shows that the two curves $f(a)$ and $f(r)$ are congruent, and Leibniz wanted to find a way of obtaining the elements he deduced from the diagram and its symmetry by calculation alone.
This text shows in a remarkable way how the resolutely formalist attitude of the German philosopher only implies a mistrust of geometric diagrams, and yet remains largely based on another diagrammatic practice: that of tables.