Transcription of De Curva Perraltii (1677–1693)
DE CURVA PERRALTII
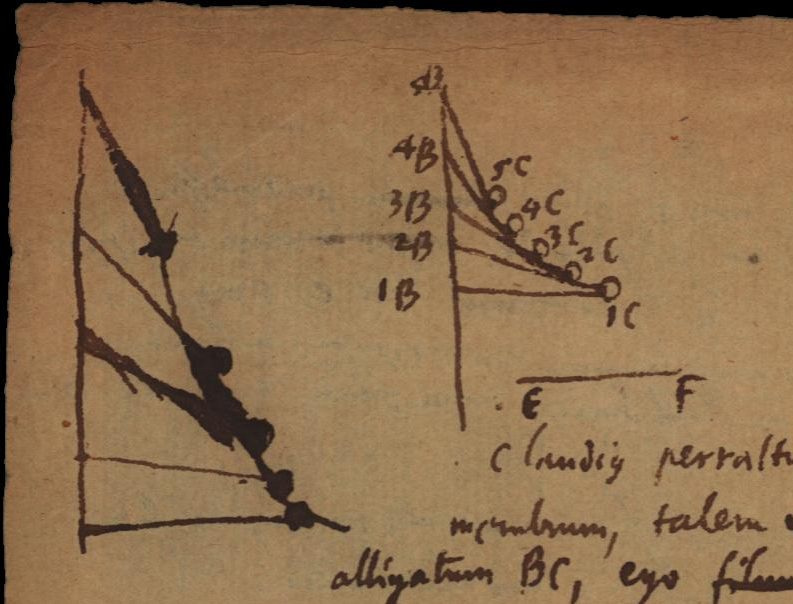
Claudius Perraltus editor Vitruvii, idemque Academiae Scientiarum Regiae membrum, talem mihi aliisque curvam investigandam proposuit. Sit corpus [latex]C[/latex] filo alligatum [latex]BC[/latex], ego fili extremitatem [latex]B[/latex] apprehendens manu, ducensque per rectam [latex]1B2B3B4B5B[/latex], cogo corpus [latex]C[/latex]. sequi; sed quia linea [latex]BC[/latex] non est rigida, sed filo flexili constans, ideo extremitas [latex]C[/latex] non fertur parallela ipsi [latex]B[/latex], sed ob corporis [latex]C[/latex] resistentiam nonnihil retardatur; quaeritur quae sit linea [latex]1C2C3C4C5C[/latex].
Solutionem ei hactenus nemo dedit, ego talem reperi. Considerandum est manum [latex]B[/latex] non movere secum corpus [latex]C[/latex], nisi quatenus ipsum trahit, id est quatenus corpus [latex]C[/latex] in eadem recta movetur in qua manus, seu manum sequitur, non vero quatenus movetur in parallela seu manum comitatur. Unde si filum semper facillime allongari posset, corpus [latex]C[/latex] manum [latex]B[/latex] nullo modo sequeretur, cum tamen esset eam filum comitaturum si filum rigidesceret, licet posset allongari.
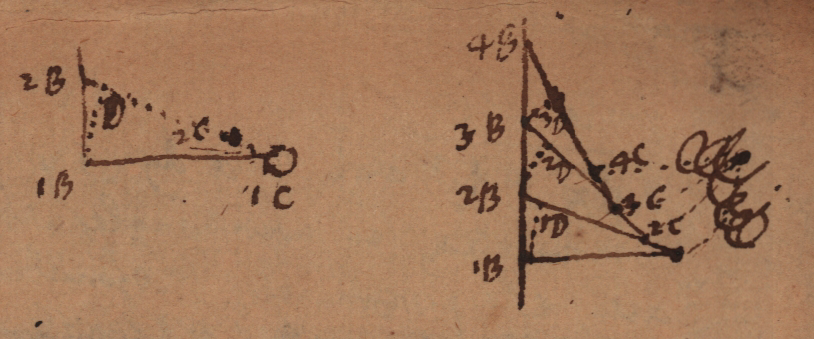
Unde motum manus ex duobus consideremus compositum, uno quasi circa [latex]C[/latex] in arcu [latex]1BD[/latex], quo nihil agit in corpus [latex]C[/latex], altero ex [latex]D[/latex] in [latex]2B[/latex], quo secum corpus [latex]1C[/latex] trahit in [latex]2C[/latex]. Unde patet rectam [latex]2B2C[/latex] esse curvae [latex]CC[/latex] tangentem, quae cum sit semper eadem, aequalis scilicet longitudini ipsius fili, habemus ergo Curvae [latex]CC[/latex] naturam talem, ut tangens [latex]BC[/latex] inde producta ad axem [latex]BB[/latex], sit semper aequalis datae rectae [latex]EF[/latex]. Quod quidem rigorose demonstrare possum si fingam manum ducentem moveri non in recta [latex]1B2B3B4B[/latex], sed in composita ex arcubus ex rectis [latex]1B1D2B2D3B3D4B[/latex], hoc enim supposito manifeste oritur quod diximus. Potest enim supponi nam positis rectis [latex]1B2B[/latex], [latex]2B3B[/latex], etc. infinite parvis, adeoque et arcubus infinite parvis [latex]1B1D[/latex], [latex]2B2D[/latex], [latex]3B3D[/latex], etc. utique manus a recta [latex]BB[/latex] non recedit, nisi intervallo infinite parvo, sive nullo intervallo. Constat etiam rectam quae duo curvae puncta intervallo infinite parvo a se remota jungit, nempe [latex]1C2C[/latex], vel [latex]2C3C[/latex] semper esse tangentem.
Res ergo reducta est ad hoc problema Geometricum, invenire curvam cujus tangentis portio inter curvam et axem intercepta sit data seu erit: [latex]\sqrt{\overline{dx}^2+\overline{dy}^2}:dy::a:y[/latex]. seu [latex]\overline{dx}^2+\overline{dy}^2:dy^2::aa:yy[/latex] seu [latex]\overline{dx}^2\smile\overline{dy}^2[/latex],[latex]+1[/latex] aequ. [latex]aa\smile{yy}[/latex] seu [latex]\overline{dx}^2\smile\overline{dy}^2[/latex] aequ. [latex]aa\smile{yy}[/latex], [latex]-1[/latex] seu [latex]\overline{dx}^2\smile\overline{dy}^2[/latex] aequ. [latex]\overline{aa-yy}[/latex], [latex]\smile{yy}[/latex], seu [latex]dx[/latex] aequ., [latex]\frac{dy}{y}\sqrt{aa-yy}[/latex].
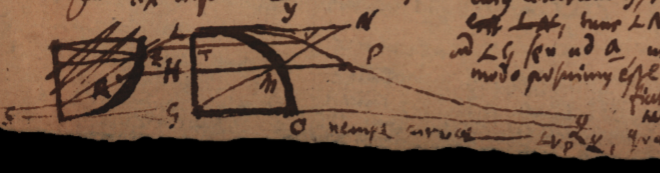
Faciamus [latex]\omega:a::dx:dy[/latex] et quadrante circuli descripto [latex]LMO[/latex] cujus centrum [latex]G[/latex], radiusque [latex]GM[/latex] sit [latex]a[/latex]: et [latex]GH[/latex] sit [latex]y[/latex]. [latex]HMsqrt{aa-yy}[/latex], tunc [latex]LN[/latex] seu tangens arcus [latex]LM[/latex], erit [latex]\omega[/latex], est enim [latex]LN[/latex] ad [latex]LG[/latex] seu ad [latex]\underline{a}[/latex], ut [latex]HM[/latex] ad [latex]HG[/latex] seu ut [latex]\sqrt{aa-yy}[/latex] ad [latex]y[/latex]. At eodem modo posuimus esse [latex]\omega[/latex] ad [latex]a[/latex], nempe ut [latex]dx[/latex] ad [latex]dy[/latex] seu ut [latex]sqrt{aa-yy}[/latex] ad [latex]y[/latex]. Fiat in [latex]HM[/latex] producta [latex]HP[/latex] aequal. [latex]LN[/latex], erit [latex]LPQ[/latex] curva tangentium. Describatur alia [latex]LZRS[/latex] curvae tangentium, nempe curvae [latex]LV PQ[/latex], quadratrix, ita ut fit [latex]TZ[/latex] ad [latex]HR[/latex] ut [latex]LTV L[/latex] ad [latex]LHPV L[/latex], tunc ordinata [latex]TZ[/latex] vel [latex]HR[/latex] erit [latex]x[/latex], quia [latex]dx[/latex] ad [latex]dy[/latex] ut [latex]\omega[/latex] ad [latex]a[/latex].
[On the side:] Brevissime [latex]C[/latex] non movetur nisi tractione, tractione autem sequitur filum in eadem recta. Jam Motus est in tangente, ergo filum est tangens. Notabile nihil referre parum an multum corpus [latex]C[/latex] motui renitatur modo cogatur sequi et filum non
extendatur.
Patet etiam quia [latex]\sqrt{\overline{dx}^2+\overline{dy}^2}:dy::a:y[/latex]. seu quia est [latex]\sqrt{\overline{dx}^2+\overline{dy}^2}[/latex] aequ. [latex]ady\smile{y}[/latex] Elementa hujus curvae esse progressionis harmonicae, seu proportionales ordinatis Hyperbolae, et proinde curvae ipsius arcus esse proportionales Logarithmis, posito abscissas [latex]GH[/latex] esse aequales numeris posito logarithmos omnes esse infinitos, sed si logarithmos incipiamus ab [latex]L[/latex]. Licet numerorum a [latex]SG[/latex] logarithmi omnes erunt finiti, excepto logarithmo nihili, qui infinitus.
Memini jam me in alia scheda quaerentem Curvam cujus arcus essent Logarithmis proportionales, invenisse ejus hanc fore proprietatem, ut portiones tangentium inter axem et curvam semper essent constanti aequales, et porro quaerendo invenisse hanc curvam fore quadratricem Tangentium, et vero patet ejus determinationem analyticam pendere ex quadratura Hyperbolae seu constructioni Logarithmorum; at ejus determinatio Organica, seu descriptio per Motum continuum hoc modo reperta est.
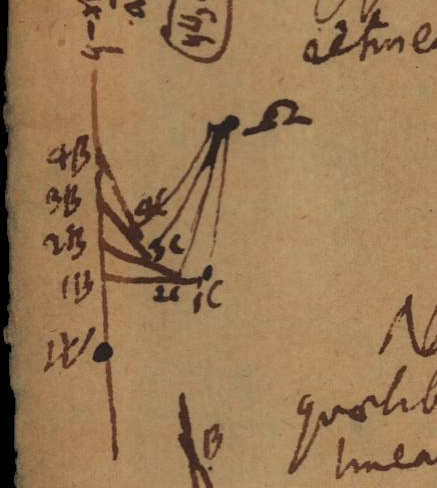
Notandum est sive corpus [latex]C[/latex] pondere suo, sive asperitate medii, sive appressione, sive Elaterio retineatur semper eandem fore curvam. Ut si corpus [latex]\Omega C[/latex] ponatur esse Elasticum cujus extremum unum [latex]\Omega[/latex] sit fixum, ita ut nec circa centrum [latex]\Omega[/latex] moveri possit, hinc motu manus filum [latex]BC[/latex] adducente sequetur punctum [latex]C[/latex], et arcus [latex]\Omega 1C[/latex] rectus, in [latex]\Omega 2C[/latex] erit flexus nonnihil, in [latex]\Omega 3C[/latex] ad huc magis et ita porro, quamdiu [latex]C[/latex] propius accedit ad [latex]\Omega[/latex].
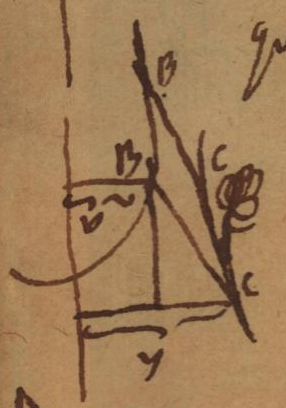
Notandum, si [latex]BB[/latex] non sit recta sed curva quaelibet, semper tamen portionem tangentis ipsius lineae [latex]CC[/latex] interceptam inter lineam [latex]BB[/latex] et lineam [latex]CC[/latex] fore aequalem datae [latex]EF[/latex]. Ordinata lineae [latex]BB[/latex] sit [latex]\upsilon[/latex]. Fiet: [latex]\sqrt{\overline{dx}^2+\overline{dy}^2}:dy::a:y-\upsilon[/latex]. Ubi cum [latex]\upsilon[/latex] pendeat ex [latex]x[/latex]. ex parte. Inventio curvae analytica fit perdifficilis, at descriptio hac eadem Methodo facillime habetur, tantum ducendo manum per lineam [latex]BB[/latex].
Imo si ponatur ipsa [latex]BC[/latex] portio tangentis intercepta continue crescere in certa ratione seu relatione ad [latex]WB[/latex] hoc modo habebitur curvae descriptio.
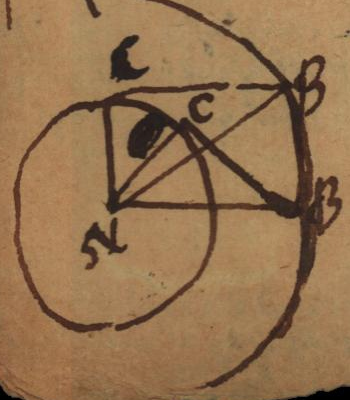
Elegans observatio si curva [latex]BB[/latex] quam percurrit manus sit circulus, curva [latex]CC[/latex] erit etiam circulus, et quidem concentricus priori et minor; sed requiritur ut constans [latex]BC[/latex] sit minor circuli [latex]BB[/latex] radio.
NB. generaliter possum hoc problema solvere, qualis debeat esse linea [latex]BB[/latex] ut curva [latex]CC[/latex] fiat data. Ex. gr. debet [latex]CC[/latex] esse recta, tunc [latex]BB[/latex] erit etiam recta, et initio incidet in situm fili.
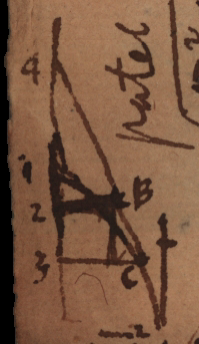
Ut [latex]1C[/latex] fiat parabola. Sit [latex]C[/latex] parabola, erit [latex]1B[/latex] data. [latex]43[/latex] aequ. bis [latex]13[/latex] seu [latex]2x[/latex]. [latex]3C[/latex] aequ. [latex]\sqrt{2ax}[/latex]. Ergo [latex]4xx+2ax[/latex] aequ. [latex]\overline{C4}^2[/latex] Sit [latex]12[/latex] aequ [latex]z[/latex]. et [latex]2B \upsilon[/latex]. jam [latex]41[/latex] est [latex]x[/latex]; fiet [latex]x+z: 4B[/latex] seu [latex]\sqrt{4xx + 2ax}-h::2x:\sqrt{2ax}[/latex]. Rursus [latex]x+z:\upsilon::x-z:\sqrt{2ax}-\upsilon[/latex]. [latex]\overline{x-z}^2+\overline{y-z}^2[/latex] aequ. [latex]a^2[/latex]. [latex]y-\upsilon[/latex] aequ. [latex]\sqrt{aa-\overline{x-z}^2}[/latex] aequ. [latex]\upsilon\upsilon[/latex].
