Justification of the Differential Calculus

Gottfried Wilhelm Leibniz, Defense du calcul des Differences.

This section presents several texts written by Leibniz in the context of the famous “Querelle des infiniment petits”, that agitated the French Académie royale des Sciences, after the attacks launched by Michel Rolle and Thomas Gouye in 1700. Leibniz first sent a letter which was published almost in extenso in the Mémoire de Trevoux [Leibniz 1701b]. However, this text raised a lot of perplexity, even amongst Leibniz’ supporters, since it contained a comparison between the various orders of differentials and fixed and finite entities such as a grain of sand and the sun (GM V 96). Being asked about these comparisons by Varignon, Leibniz replied in the famous letter of 2 February 1702, that it was a coarse way of speaking and that infinitesimals should not be seen as fixed entities (published in the Journal des Sçavans [Leibniz 1702]). The Justification was conceived as a follow up to this letter aimed specifically at critique coming from Rolle. It was sent again to Pinsson for Varignon for publication in the Journal des Sçavans, but the project did not succeed. The Cum Prodiisset, written at the same period, provides a different strategy for the foundation of the differential calculus (based not only on the law of continuity, but also on the use of varying ratios of finite quantities). The beginning of The Defense du calcul summarizes these various strategies and testifies to Leibniz’ pluralistic approach to the justification of his calculus.

Overviews

Cum prodiisset ([LH 35, VII, 19, Bl. 1-6])

Overview of Cum prodiisset (>1702)

The Cum Prodiisset manuscript was first published by Gerhardt, with no indication of its date and a few transcription errors [Leibniz,1846]. Child proposed an English translation in 1920 [Child, 1920, pp. 144-158]. He dated the manuscript from the time of the controversy with Bernard Nieuwentijt (1694-1695). This dating is not satisfactory since at the beginning of the text, Leibniz refers to the article by Thomas Gouye published in the Journal des Sçavans in May 1701 [Gouye 1701] and then to Hermann's answer to Nieuwentijt [Hermann, 1700]. Additional evidence suggests that Cum Prodiisset is, in fact; intimately related to the twin texts presented in this section : Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire and Defense du calcul des différences... view

Puisque des personnes que j’estime beaucoup ([LH 35, VII, 9, Bl. 1-2])

Overview of Puisque des personnes que j’estime beaucoup (1705)

This manuscript is a shortened French version of Sentiment de Monsieur Leibnitz (available here). It was probably intended for the Parisian savants (the other, in Latin, being reserved for publication in the Acta Eruditorum).

view
Sentiment de Monsieur Leibnitz ([GOTHA Forschungsbibliothek, Chart. A 448-449, Bl. 41-42])

Overview of Sentiment de Monsieur Leibnitz (1705)

In July 1700, at the Académie royale des sciences, the algebraist Michel Rolle launched the first criticisms against differential calculus, based on its foundations and on its use which he thought fraudulent. This intervention marks the beginning of the well-known querelle des infiniment petits. The Sentiment de Monsieur Leibnitz manuscript bears witness to one of the last episodes of this quarrel before its appeasement in 1706.

In 1705 the debate was at its peak. In his essay Remarques de M. Rolle de l’Académie des Sciences touchant le problesme général des tangentes [Rolle, 1703], Rolle completely discredited both the foundations and the exactness of differential calculus Two years later, on 23 April 1705, Saurin published a reply [Saurin 1705] which he ended by imploring the Académie to pass judgment on the discrepancies between him... view

Quaestio de jure negligendi quantitates infiniti parvas ([LH 35, VIII, 21, Bl. 1-2])

Overview of Quaestio de jure negligendi quantitates infiniti parvas (> 1702)

This manuscript has been already transcribed by Pasini (App., [Pasini 1985, 40-47).

One of the main interests of Quaestio de Jure is that it contains most of the arguments put forward by Leibniz to legitimize his calculus between 1701 and 1702. Moreover, Leibniz made an allusion to “ingeniosissimos viros” just before developing examples, which are based on series and which illustrate the computational intractability of zero and infinity when considered as absolutes. These developments are extremely close to those exchanged in October 1702 with Philip Joseph Jenisch [LH 35, 7, 17, 2ro-5ro] and Philippe Naudé [LH 35, 7, 17, 7ro] (transcribed both in App. [Pasini 1985, 19-31] and [AIII 9, 216-226]. This provides a terminus a quo for the dating of our text.

The main criticism of Leibniz’ calculus is the question of the elimination of infinitely small quantities of any order during the computing process. This criticism is crucial because it is intimately linked to the status of... view

Qvelques remarques sur les Memoires de Trevoux de l'an 1701 ([LH 11, 6, Bl. 3-4])

Overview of Qvelques remarques sur les Memoires de Trevoux de l'an 1701 (1702)

The Mémoires pour l’histoire des sciences et des beaux-arts, better known as the Journal de Trévoux or Mémoires de Trévoux, is a journal founded by the Jesuits in 1701 in Trévoux. This bimonthly publication was composed of articles on various literary, scientific and religious topics.

As soon as the first issues of the Journal appeared, Leibniz wished to be kept informed of articles published in it and he obtained them through his friend François Pinsson. His interest was aroused by certain articles and he did not hesitate to send his point of view to the Journal on many occasions.

The present text... view

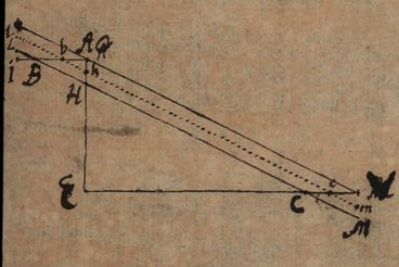
Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire ([LBr. 951, Bl. 15-16])

Overview of Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire (1702)

There are three versions of the text we present: the manuscripts LBr. 951, Bl. 14, LBr. 951, Bl. 12-13, LBr. 951 Bl. 15-16. The last one has already been edited by Gerhardt [GM IV, 104-106]. We will offer soon a new transcription integrating the variants which seem significant to us.

This text is to be situated among a series of responses that Leibniz formulated particularly for the attention of the members of the Académie des sciences during la querelle des infiniment petits. Indeed, barely one year earlier, in a short article in the Journal de Trévoux [Leibniz 1701b], Leibniz had explained that the practice of his calculation did not require taking the infinitely small in a rigorous way, but that it was sufficient to consider quantities as small as needed. This way of proceeding differs from the manner of the Ancients, he argued, only in the “expressions”. Using the examples... view

Defense du calcul des Differences ([LH 35, VI, 22, Bl. 1-2])

Overview of Defense du calcul des Differences (1702)

Defense du calcul des Differences is clearly to be situated at the same time and in the same context as Justification du Calcul des infinitésimales par celuy de l’Algèbre ordinaire which we also present in this section (available here). While the notation is different, their developments are based on identical geometric configuration.

It is possible that Leibniz wrote Justification first and then used it later to write a longer text in which he kept the same example. Indeed, although very similar, Defense du calcul des Differences, unlike Justification, contains a preamble in which Leibniz announces his intention to show that in his calculus the elisions of infinitely small quantities are not made in an arbitrary manner as argued by "des personnes habiles qui s’opposent au... view