Overview of De Angulis Curvarum
"De Angulis Curvarum", as well as "De Angulo contactus et curvedine et de natura quantitatis", was most probably written after 1682 – since the conceptual elaborations on curvature are more advanced than in “Multa et mira de Angulo contactus”, but a little before June 1683 – since we find in "De Angulis Linearum plane nova" a reprise of the issues dealt with in the three manuscripts.
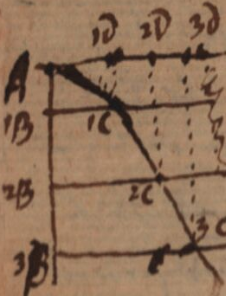
Leibniz introduced the concepts of convexity/concavity and that of the direction of a curve by means of kinematic considerations – considerations that can be found in later writings, such as "Specimen geometriae luciferae" (Gerhardt, GM, VII). The idea is to consider a curve as resulting from a double rectilinear motion: that of a point moving along a straight line, which itself parallel to itself maintaining the same angle with respect to a second given line.
The tangent at a point of the curve is the direction that this point would take, endowed with the resultant of the two velocities, at the moment when their external cause ceases to act. This observation allows Leibniz claims that we can consider that the angle made by two intersecting curves is the same as the rectilinear angle between their two tangents, and that therefore the angle of contact can be considered to be null in respect to the rectilinear angle.
It is only when the two curves are tangent that the comparison of the angles of contact is of any interest, since in this case, Leibniz states that the angle they make is considered to be the same as that made by two particular tangent circles. Each of this pair of circles has the same angle of contact as the respective curve has with its tangent, and consequently – Leibniz claims – it has the same curvature.
As in “Multa et mira de Angulo contactus”, Leibniz seeks the circle of the same curvature by relying on diagrammatic considerations: it is the tangent circle with the greatest radius of all the circles that fall inside the curve and such that if its radius is increased a little, it will fall outside the curve. Here, he also oscillates on the number of roots needed - three or more - to determine the osculating circle (this designation as well as “angle of osculation” is made in the margin of the page).

In “De Angulis Linearum plane nova” and in the article from Acta Eruditorum “Meditatio nova de natura anguli contactus et osculi” (Leibniz, 1686), Leibniz did not present any computation, but formulated what he designated as a "Theorema memorabile": at the vertex of a conic, the radius of the osculating circle is equal to half the latus rectum. In the "De Angulis Curvarum", we find the computations that were necessary for Leibniz to obtain this result. Furthermore, Leibniz also obtained by calculation the equation of the locus of the centers of curvature of the ordinary parabola, which he identified - for the first time, it seems – with the evolute of the curve in this particular case but, more importantly, in the general case.
