Overview of De Angulis Linearum plane nova
"De Angulis Linearum plane nova" appears to be the result of the research conducted in the three manuscripts "Multa et mira de Angulo contactus" and especially "De Angulis Curvarum" and "De Angulo contactus et curvedine et de natura quantitatis". To begin with, in the top right margin, Leibniz writes that with this scheda he has summarised matters concerning the angles of curved lines in a "complete and clear" manner. Indeed, from the very first lines, he announces that he is intending to show that the angles of the curves - which he immediately names "angles of osculation" - are of any degree, incomparable from one degree to another. To every degree of osculation corresponds a curve of osculation: first the circle followed by "ellipses" of any degree. In the following, he develops most of the questions dealt with in the other three manuscripts, but unlike "De Angulis Curvarum", he does not carry out any computation.

Leibniz continues to characterise the osculation circle as the one which, among tangent circles, is the most 'tightly' connected to the curve and the last [ultimum] to remain strictly in the curve. He also states his "Theorema memorabile": at the vertex of a conic, the radius of the osculating circle is equal to half the latus rectum.
However, he no longer hesitates to state that the osculating circle is obtained not by equality of three roots but of four roots. His insistence on this subject is such that he presents the idea of a method of determination of the circle of osculation considering it as passing through four coincident points of the curve.
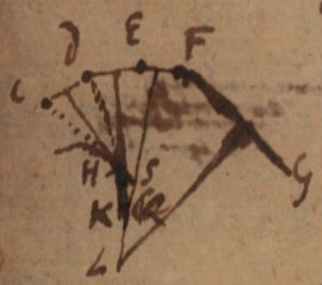
This method consists in determining the centre of the circle as the intersection of three pairs of perpendiculars to segments whose extremities are points infinitely close. In fact, this method is a modified version of the method of determining the evolute of a curve, and again testifies to the fact that around 1683, Leibniz was aware of the identity between the locus of the centres of the circles of osculation of a curve and its evolute.
