Manuscripts on Dyadica
This section contains Leibniz’s unpublished manuscripts concerning his studies on the binary numeral system or dyadics, as he called it. While Leibniz is rightfully considered the discoverer of the binary numeral system, or at least of its importance in a computational context and is thus the father of today’s computer science, of the over 170 manuscript sheets concerning dyadics less than 10% of them have been transcribed at the time of writing, oftentimes without a proper critical edition. Leibniz started working on dyadics in around 1679, as is believed from one of the earliest manuscripts, De Progressione Dyadica, dated 15 March 1679. Even though Leibniz’ production on dyadics spans his life, he never really showed publicly his most complex results on this topic, probably because he thought they were too far from what was usually debated during those times in mathematical circles. Despite this reluctance, he was, on a more general level, a keen advocate of the importance of the new numeral system, as it is shown for example by his discussions with the Bernoulli brothers (A III, 8, N. 233) or his correspondence with Joachim Bouvet on the connection between dyadics and the Chinese I Ching (A I, 19, N. 202, A I, 20, N. 318-319), which culminated with the publication of the Explication de l'arithmétique binaire for the Académie royale des sciences in 1703 (LBr. 68, 21r). As the way in which Leibniz develops dyadics is a unique case of a direct relationship between metaphysics and mathematics, he often discusses the topic from a philosophical standpoint: the correspondence between Leibniz, Rudolf Augustus, Duke of Braunschweig-Wolfenbüttel, and Müller on the possibility of producing a coin representing the connection between 1 and 0 and unity and nothingness is the most famous example of this relationship (LBr. F 15). The collection presents manuscripts relating mostly to Leibniz’s mathematical achievements: the foundation and development of binary arithmetic, studies on the binary expression of numbers and on the binary expansion of their squares.
De Progressione Dyadica
Overview of De Progressione Dyadica (1679)
De Progressione Dyadica is probably the most famous manuscript concerning the development of the binary numeral system. It is dated by Leibniz himself (15 March 1679) and is thus considered the earliest reliable document on this topic, but at the same time, no one has yet offered a complete transcription of it: it is in fact only mentioned by Couturat [Leibniz 1903, 574] as early as 1903, while in 1966 a facsimile of the manuscript with an incomplete German translation appeared in Leibniz [1966].
The manuscript is divided into two parts: the first focuses on the binary numeral system in general, its properties and its binary arithmetic, while the second introduces an innovative method of discovering mathematical truths through a unique combination of algebra and binary numbers, defined by some scholars as binary algebra.
At the beginning of the first part, Leibniz presents a progression of numbers from 1 to 32, written both in the decimal numeral system and in the binary numeral system. He clearly identifies the connection between the position of a digit and its expression as a power of 2 in the binary system. This insight is particularly relevant because it is the premise for what in today’s terms, we would call a positional notation, where a single number is treated as a series of sums having a fixed order in which a change of position from right to left also represents an increase of the base index.
This general introduction is then followed by the description of a method to obtain the binary counterpart of a decimal number through multiple divisions by two:
Every time a number cannot be divided by two, we divide the closest divisible number and we write 1 as a carry, while every time a divisible number occurs, we write 0: in this way we progressively obtain the same number, expressed however in its binary form, as shown in [Fig. 1]. Leibniz also describes the four common arithmetical operations, showing the best way to implement them with binary numbers.
At the end of the first part Leibniz shifts from arithmetic to algebra. He starts to consider letters instead of numbers for his explorations, adding an important condition that is generally not followed in ordinary algebra: these letters can only represent either the number 1 or the number 0, in the context of the binary numeral system. Leibniz’s aim is to show that while there are some general algebraic properties that are both applicable in the context of the decimal and the binary numeral system, new unique relations between numbers could be found if we focus solely on the latter. This is the case of the expansion of a square in a sum of numbers, explored at the beginning of the second part of De Progressione Dyadica. While we can describe algebraically the expansion of a square in a form which is valid regardless of the numeral system adopted, Leibniz shows that there is an alternative version of this expansion which is valid only for the binary numeral system. A detailed explanation of why this is possible is present in Brancato (2021).
The last section of the second part is dedicated to the binary expression of fractions and their involvement in the expression of [latex]\frac{\pi}{4}[/latex] as a series of sums, a topic Leibniz will frequently connect with dyadics. In the considerations on transcendental quantities present at the end of De Progressione Dyadica we witness here the premise to the great reflection on the possibility of expressing any type of number in the binary numeral system, which became one of Leibniz’ main focuses throughout his production on dyadics.
Periodus numerorum
Overview of Periodus numerorum (1705?)
Periodus Numerorum is a manuscript written by Overbeck for Leibniz in around 1705 and represents a collection of results obtained by Leibniz on the topic of dyadics. The content of the manuscript strongly suggests that it was dictated word by word by Leibniz, as that level of knowledge of the binary system it includes was available only to him at that time.
The manuscript starts by introducing a new notation to express what had already been defined by Leibniz in other manuscripts as the period of natural numbers:
[latex]0_{1024}1_{1024}|0_{512}1_{512}|0_{256}1_{256}|0_{128}1_{128}|0_{64}1_{64}|0_{32}1_{32}|0_{16}1_{16}|0_{8}1_{8}|0_{4}1_{4}|0_{2}1_{2}|0_{1}1_{1}=N[/latex]
[latex]20\ \ \ \ \ \ \ 19\ \ \ \ \ \ \ \ \ \ 18\ \ \ \ \ \ \ \ \ 17\ \ \ \ \ \ \ \ \ 16\ \ \ \ \ \ \ \ 15\ \ \ \ \ \ \ \ 14\ \ \ \ \ \ 13\ \ \ \ \ 12\ \ \ \ 11\ \ \ 10[/latex]
What Leibniz means with this notation is that any natural positive integer can be written in a dyadic form, keeping in mind that every digit (presented from right to left) will also belong to a period of alternating zeroes and ones, as shown in the tables of De progressione dyadica, or as represented here by the number of repeating zeroes and ones specified by the subscripts. In fact, if we write the progression of every positive integer in the form of a table we obtain the same period expressed by Leibniz in his new notation:
The text then shifts its attention from this new unique way of expressing these numbers to their algebraization, following the development of De progressione dyadica manuscript. This time however, instead of using generic letters for the algebraization, Leibniz choose to implement numbers having the function of algebraic letters, a method he had already used in another manuscript published by Zacher (the Summum calculi analytici fastigium), to better convey the fact that there can be as many digits in these numbers as we want, as they are positive integers of an infinite set.
Once these numbers, also called fictive numbers in the mathematical tradition, are assigned to every binary digit, Leibniz shows the relationship between two algorithms for the expansion of a square, the first one valid in any numeral system and the second one valid only for the binary numeral system, following again the Summum calculi analytici fastigium (Zacher 1973, 220):
The first table shows the expansion of a square in the form [latex](a+b…)^2[/latex], while the second describes another expansion valid only for numbers expressed in the binary system. This result is relatively independent from the rest of the manuscript, because it can be obtained ignoring the new notation for the periods introduced by Leibniz, as in fact he does in De progressione dyadica. For a more detailed explanation of the relationship between these two algorithms see Brancato (2021).
Shifting the attention once again to the new way of expressing the period of positive integers presented at the beginning, the manuscript then introduces some laws of calculation valid only in the binary numeral system. In this part of the manuscript Leibniz tries to apply his own rules to describe multiplications and additions between fictive numbers representing periods:
The main idea is that if belonging to a particular column means that a digit has a probability of being 0 or 1 following a certain pattern, investigating the relationship of addition and multiplication between digits belonging to different columns is a legitimate way to determine the new pattern followed by the digit that will be obtained as a result of this combination. These explorations lead Leibniz to a general rule connecting fictive numbers and periods: [latex]1m\times1n=0_{2^m}\left(0_n1_n\right)_{2^{m-n-1}}[/latex], where m and n represent any possible second part of a fictive number.
Tentata Expressio Circuli Per Progressionem Dyadicam
Overview of Tentata Expressio Circuli Per Progressionem Dyadicam
This manuscript, dated around 1680, is particularly important in the context of the evolution of Leibniz’s work on dyadics, because it shows once again that the major developments in his approach happened after 1679 are connected with its study on the expression of a circle having diameter 1 (π/4) in the form of Gregory’s series.
This study is a comparison between a dyadic progression, expressed in the form :
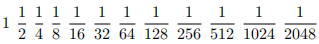
and called dyadic because it has powers of 2 at the denominator, and the standard Gregory series expressed in the form
Initially, the connection between the two series might not be as evident, but during that time Leibniz had discovered that, if we express all the natural numbers in a binary form one after the other or we express all the odd positive integers in this way, we will see that the periods of ones and zeroes formed by reading these lists vertically is the same:
Since the former list can be associated easily to the first progression, while the second appears at the denominator in Gregory’s progression, Leibniz was convinced that through a series of manipulations one would be able to establish a connection between the two.
This manuscripts represents one of these attempts in finding possible relations between the two progressions. Leibniz strategy here is first to compare finite portions of the progressions and, since it is not possible to state that they are equal, at least see if one portion is greater or less than another one. Secondly he compares the portions to the Gregory’s infinite progression and establishes if the dyadic portions analyzed are greater or less than the expression of the entire circle. For instance, if $\frac{1}{2}$ is less than $1-\frac{1}{3}$ and $1-\frac{1}{3}$ is less than the value of the circle, then $\frac{1}{2}$ is less than the value of the circle.
After some experimentation in this direction, the manuscript ends with a standard analysis of the binary system, presenting the list of natural numbers expressed in the binary system and the calculation of some fractions.
Diophantea seu Arithmetica figurata absoluta methodo dyadica
Overview of Diophantea seu Arithmetica figurata absoluta methodo dyadica
Despite being a small fragment, manuscript LH 35 3 A 16 Bl. 27 represents an important part of Leibniz’s corpus on dyadics. It was first published by Couturat in Opuscules et fragments inédits de Leibniz (1907, 571) with a fairly precise transcription, albeit small mistakes.
Its importance comes first from the fact that Leibniz himself highlights here the result he achieved by writing before the text multiple times the word “NB”, i.e. “Nota Bene”. At the same time, we don’t witness in the manuscript a major breakthrough in the evolution of the binary system: here, as much as in many other places, the superiority of dyadics is connected with the possibility of dealing with a number’s power in an easier way than in the decimal system, provided we express numbers in an indefinite dyadic form (a possible reference to what I defined as binary algebra). Since this approach is present in Leibniz’s production since the very beginning, connecting these two observations (the enthusiasm showed by Leibniz about his results and the fact that they are among the first he obtained) we could cautiously infer that this might be one of the first manuscripts in which Leibniz realizes dyadics’ great potential on the matter, suggesting a possible dating between 1676 and 1679. A later dating is suggested by Alcantara, following Couturat (J. Alcantara, « cette caractéristique secrète et sacrée… » : Leibniz et Bouvet, lecteurs du yijing, Intervention au séminaire du Centre d’Études et de Recherches sur l’Humanisme et l’Âge Classique, UPRES-A CNRS 5037, équipe de recherche du Centre International Blaise Pascal, Chiffres et secrets, organisé par M. Dominique Descotes, 21 janvier 2006, Université de Lyon III), but this is probably due to the fact that evidences of Leibniz’s work on dyadics before 1679 were found only recently.
Another important element present in the manuscript is the explicit connection between dyadic and what Leibniz calls Diophantea or Arithmetica Figurata, a connection which is already evident mathematically throughout Leibniz’s whole production, but rarely made this explicit.
The fact that Leibniz was interested in Diophantine equations is largely proven by his works and his knowledge of Fermat’s works. The connection with dyadic becomes particularly important if we compare Leibniz’s use of the binary system with the contemporary notions of Diophantine geometry, algebraic geometry, arithmetic geometry, and number theory. There is in fact here more than a simple reference to arithmetic, as Couturat suggested in his La logique de Leibniz (1901, 293), because the equivalence between Diophantine problems and Figurative Arithmetic problems highlighted by Leibniz is not only a reference to the fact that in such topics we use and study geometric progressions and geometric series: Figurative Arithmetic is also involved in the study of figurative numbers, as intended by the Pythagorean tradition. In Leibniz’s mind then, the work on Diophantine equations is also a way to prove the relevance ofthis tradition and, above all, a way to promote his own, more sophisticated version of an arithmetic connected to geometrical representation and yet founded on the binary system: as much as Pythagoras’ figurative numbers were highlighting mathematical relations through the study of their geometrical representation and position, so Leibniz’s Arithmetica Figurata based on dyadics highlights in the best way possible mathematical relations that can be expressed by Diophantine equations. This is consistent on one side with Weigel’s early Pythagorean influence on Leibniz and on the other side with Leibniz’s superior mathematical knowledge with respect to his former teacher, paving the way to his own evolution of these traditional topics.
Appropinquatio Circuli Per Radices Dyadice Expressas
Overview of Appropinquatio Circuli Per Radices Dyadice Expressas
The first part of this manuscript, dated between 1683 and 1685, is a reflection on the formula that gives the perimeter of a regular polygon inscribed in a circle. Since Leibniz shows that the formula depends on powers of 2, we could use dyadics to help in the calculations.
In this reflection Leibniz combines two strategies already utilized in other manuscripts: the notion that powers of 2 simplify the calculations, i.e. in this case the fact that the product between a number and a power of 2 entails always the addition of 0, and the notion that 10.00000... is equal to 1.11111... . Leibniz states then that the extraction of 1.11111 ... is easier than the extraction of 10, meaning that we are allowed to substitute it in the $\sqrt{2}$ progression created.
This is one of the few cases in which these two results usually connected to dyadic are combined.
The second part of the manuscript may appear less interesting, because we find here a study on the progression of the algorithm for the expansions of the squares, as it is already found in manuscripts like Periodus numerorum. In this manuscript however, the generalized progression of the squares is used to show that the second digit of a squared number written in binary form is always 0. While this result is present in other works, for the first time here it is demonstrated through calculations using binary algebra and not derived by a simple hypothetical reasoning.
Notae Ad Arithmeticam Et Dyadicam
Overview of Notae Ad Arithmeticam Et Dyadicam [1676 (?)]
This manuscript is a reflection on the mathematical truth stating that from the identity $bx=by$ doesn’t follow necessarily $x=y$, unless we establish that $b$ is different from $0$. What makes the fragment interesting is the fact that Leibniz, in order to show this, appeals to binary algebra: he considers a similar algebraic identity, stressing that in this particular case the utilized letters stand for binary numbers, more precisely either the number 1 or the number 0. Just like in the general case, from the identity $p,1−ϕ=p.qu(ϕ−p)$ doesn’t follow necessarily that $1−ϕ=qu(ϕ−p)$, unless we take $p$ different from 0, i. e. equal to 1.
The use of binary algebra, even if at first might seen pointless, has here in Leibniz’s mind two advantages: it shows the same property belonging to $bx=by$, restricting however the possible value of $b$ to two, one for which the property is satisfied and another one for which it is false. This brings a kind of elegance or simplicity to the demonstration, because we are encouraged to prove the same universal truth resorting however to fewer elements, since $p$, instead of $b$, cannot be any possible number, but only 1 or 0.
The second advantage is a direct consequence of this approach: since the value assigned to the letters in the whole equation can only be ones and zeroes, substituting the various letters with their different values becomes easier, hence we can easily imagine all the possible cases. This hypothetical approach that analyses an equation through a series of possibilities is very typical of Leibniz’s binary algebra, as it is present also in manuscripts like De Progressione Dyadica and Summum Calculi Analytici Fastigium. It is particularly interesting because it merges combinatorial approach with the use of binary letters almost like truth-values, closing the gap between binary mathematics and logic.
Summa seriei binariae
Overview of Summa seriei binariae [1676 (?)]
In this manuscript, Leibniz shows that every sum in the form $2^e+2^{e-1}...+2^{e-e}$ is equal to $2^{e+1}-1$. On a surface level, this fragment might not appear related to dyadics, because no use of the binary notation is involved. However, some hints suggest its strong relation to the work on the binay system: first of all, the identity expressed is valid only for base two powers, meaning that Leibniz was searching here for properties unique to the base two system. Even more, thanks to the work on these unpublished manuscripts, it is known nowadays that Leibniz’s work on dyadic was strongly related to his work on transcendental numbers and their properties. Since, according to Leibniz, transcendental numbers are generated through a manipulation of series of powers having an indefinite number of exponents, a property like the one demonstrated in this manuscript, which can be applied to any series written in this form regardless of the value assigned to e, must have been interpreted by Leibniz as an encouraging hint that the work on the base two system could have led to the mastering of transcendental numbers.
For these reasons, it is safe to assume that this manuscript is dated around 1679: around that time in fact Leibniz’s interest towards irrational and transcendental numbers was merging with his interest in dyadic.