Overview of Tentata Expressio Circuli Per Progressionem Dyadicam
This manuscript, dated around 1680, is particularly important in the context of the evolution of Leibniz’s work on dyadics, because it shows once again that the major developments in his approach happened after 1679 are connected with its study on the expression of a circle having diameter 1 (π/4) in the form of Gregory’s series.
This study is a comparison between a dyadic progression, expressed in the form :
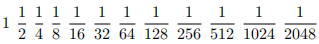
and called dyadic because it has powers of 2 at the denominator, and the standard Gregory series expressed in the form
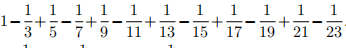
Initially, the connection between the two series might not be as evident, but during that time Leibniz had discovered that, if we express all the natural numbers in a binary form one after the other or we express all the odd positive integers in this way, we will see that the periods of ones and zeroes formed by reading these lists vertically is the same:
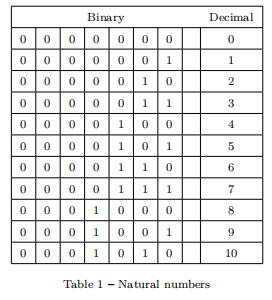
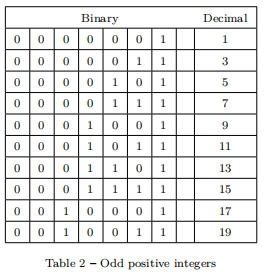
Since the former list can be associated easily to the first progression, while the second appears at the denominator in Gregory’s progression, Leibniz was convinced that through a series of manipulations one would be able to establish a connection between the two.
This manuscripts represents one of these attempts in finding possible relations between the two progressions. Leibniz strategy here is first to compare finite portions of the progressions and, since it is not possible to state that they are equal, at least see if one portion is greater or less than another one. Secondly he compares the portions to the Gregory’s infinite progression and establishes if the dyadic portions analyzed are greater or less than the expression of the entire circle. For instance, if $\frac{1}{2}$ is less than $1-\frac{1}{3}$ and $1-\frac{1}{3}$ is less than the value of the circle, then $\frac{1}{2}$ is less than the value of the circle.
After some experimentation in this direction, the manuscript ends with a standard analysis of the binary system, presenting the list of natural numbers expressed in the binary system and the calculation of some fractions.
