Transcription of Trigonometria Sphaerica Tractanda per Projectionem in Plano (1679 - 1680)

Transcription of Trigonometria Sphaerica Tractanda per Projectionem in Plano (1679 - 1680)

⟨Tri⟩gonometria sphaerica tractanda per projectionem in plano

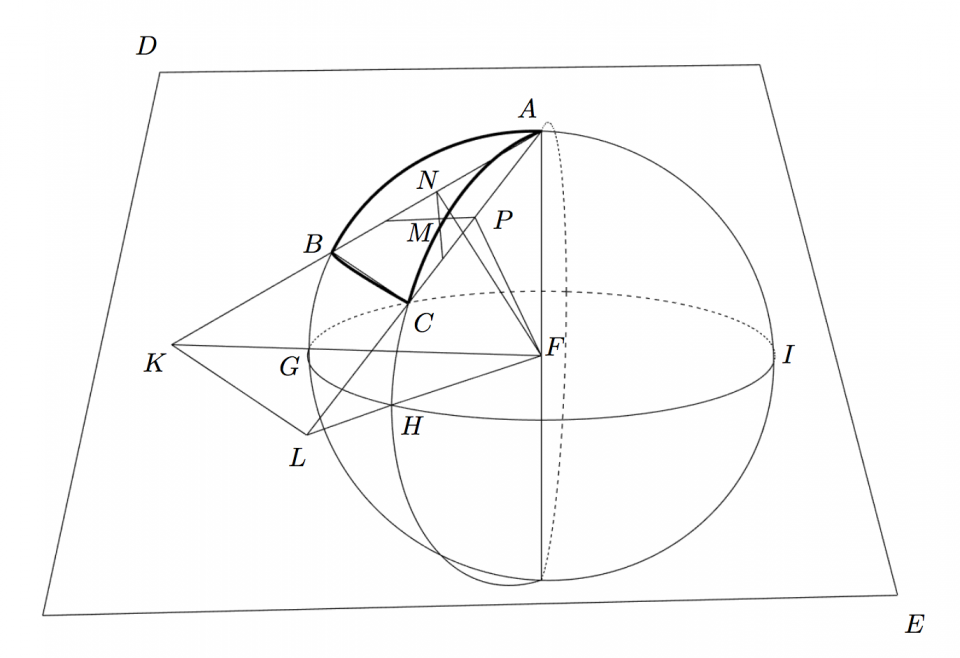
Sit Triangulum Sphaericum [latex]ABC[/latex], et planum [latex]DE[/latex] secans sphaeram in tribus punctis [latex]A. B. C.[/latex] utique projectio trianguli sphaerici [latex]ABC[/latex], erit triangulum rectilineum [latex]ABC[/latex] in plano [latex]DE[/latex] descriptum, cujus latera se habebunt ad latera sphaerici, ut chordae se habent ad suos arcus, radio [latex]FA. FB. FC[/latex], ex centro sphaerae [latex]F[/latex] semper existente eodem. Jam quia et angulos trianguli sphaerici quodammodo in plano exhibere volumus, hinc polo [latex]A[/latex] describatur aequator [latex]GHI[/latex] arcus [latex]AB[/latex], [latex]AC[/latex] productos si opus secans in punctis [latex]G[/latex] et [latex]H[/latex].

[On the side:]

[End]

Quoniam ergo omnis projectio circuli magni in plano, si ex sphaerae centro spectetur, est recta, hinc arcus aequatoris, [latex]GH[/latex] projectio in plano [latex]DE[/latex], sit recta [latex]KL[/latex]. In plano [latex]DE[/latex] jungantur puncta [latex]A[/latex] et [latex]K[/latex], recta [latex]AK[/latex] transibit per [latex]B[/latex]. et [latex]AL[/latex] eodem modo per [latex]C[/latex].

A puncto [latex]F[/latex] (sphaerae centro) ad planum [latex]DE[/latex], vel [latex]ABC[/latex] ducatur minima, quae hoc loco cadet intra triangulum [latex]ABC[/latex], quia cum sit minor quam [latex]FA[/latex] vel [latex]FB[/latex] vel [latex]FC[/latex], erit intra sphaeram, sola autem plani [latex]DE[/latex], portio [latex]ABC[/latex] est intra sphaeram. Methodus a dato puncto [latex]F[/latex] ad datum planum [latex]ABC[/latex] ducendi [latex]FM[/latex] lineam minimam posito tria plani puncta [latex]A. B. C[/latex], esse data, eorumque distantiam a puncto extra planum a quo minima quaeritur; esse etiam datam, talis erit. Datis trianguli [latex]ABF[/latex] tribus lateribus [latex]AF. AB. FB[/latex], dabitur altitudo [latex]FN[/latex], minima a puncto [latex]F[/latex], ad rectam [latex]AB[/latex], ergo dabitur et [latex]AN[/latex], ergo et punctum [latex]N[/latex], ex quo educatur perpendicularis [latex]NM[/latex], angulo [latex]MNA[/latex] vel [latex]MNB[/latex] recto.

[On the side:]

[End]

Eodem modo investigetur punctum [latex]P[/latex] in recta [latex]AC[/latex], respondens ipsi [latex]N[/latex] in recta [latex]AB[/latex], ex quo puncto [latex]P[/latex] educatur etiam perpendiculariter [latex]PM[/latex], angulo [latex]MPA[/latex] vel [latex]MPC[/latex] recto, quae duae perpendiculares se secabunt in puncto [latex]M[/latex], et [latex]FM[/latex], erit Minima, quia [latex]MN[/latex] minima ex [latex]M[/latex] ad [latex]AB[/latex], et [latex]FN[/latex] minima ex [latex]F[/latex] ad [latex]AB[/latex], ergo et summa quadratorum ab [latex]FN[/latex] et [latex]MN[/latex], hoc modo minima, ergo et [latex]FM[/latex] latus hujus summae minima. Ubi notandum si ea methodo qua [latex]N[/latex] et [latex]P[/latex] investigetur [latex]Q[/latex], in recta [latex]BC[/latex], et inde educatur normalis, ad [latex]BC[/latex], eam etiam incidere in punctum [latex]M[/latex].

Hoc loco autem, cum puncta [latex]A. B. C.[/latex] aequidistent a puncto [latex]F[/latex], puncta [latex]N. P. Q.[/latex] erunt media rectarum [latex]AB. AC. BC.[/latex] et punctum [latex]M[/latex], erit centrum Circuli triangulo [latex]ABC[/latex] circumscripti. (Habetur [latex]AG[/latex] diagonalis quadrati ab [latex]AF[/latex]. (Habetur et [latex]BG[/latex] chorda arcus [latex]BG[/latex].) Sed non opus puncto [latex]M[/latex]. Nam cum angulus [latex]GFA[/latex] vel [latex]KFA[/latex] sit rectus, et sumto puncto [latex]N[/latex] medio ipsius [latex]AB[/latex], junctaque [latex]FN[/latex] sit angulus [latex]FNA[/latex] rectus, erunt triangula [latex]AFK[/latex] et [latex]ANF[/latex] similia, et cum dentur [latex]AF, AN[/latex] (seu [latex]\dfrac{1}{2}AB[/latex]), FN[/latex], ideo dabuntur et [latex]AK, KF[/latex].

Nimirum [latex]AK : AF :: AF : AN[/latex]. Seu [latex]AK[/latex] aequ. : [latex]AF^2\smile+\dfrac{1}{2}AB[/latex]. Eodem modo [latex]AL[/latex] aequ. [latex]AF^2\smile+\dfrac{1}{2}AC[/latex]. Ergo [latex]AK : AL :: AC : AB[/latex]. Cumque [latex]AL[/latex] et [latex]AK[/latex], itemque [latex]AB[/latex] et [latex]AC[/latex], angulum comprehendant eundem in [latex]A[/latex], erunt triangula [latex]ABC[/latex], et [latex]ALK[/latex] similia, et quod notabile sub-contraria. Itaque cum dentur [latex]AF. AB. AC. BC[/latex], erit [latex]\underline{AK}[/latex] aequ. [latex]AF^2\smile+\dfrac{1}{2}AB[/latex], et de reliquo [latex]\underline{AL : AK : KL} :: AB : AC : BC[/latex].

Eodem modo habebimus et [latex]FL[/latex], nam sumto [latex]P[/latex] puncto medio rectae [latex]AC[/latex] jungamus [latex]FP[/latex], erit [latex]APF[/latex] triangulum rectangulum simile ipsi [latex]AFL[/latex], ut supra Triang. [latex]ANF[/latex] simile Triangulo [latex]AFK[/latex]. Ergo habemus [latex]FK : AF :: NF : AN[/latex]. seu [latex]FK[/latex] aequ. [latex]AF, NF\smile\dfrac{1}{2}[/latex] AB et FL[/latex] aequ. [latex]AF, NP\smile+\dfrac{1}{2}AC[/latex]. Est autem [latex]NF[/latex] aequ. [latex]\sqrt{AF^2–\dfrac{1}{4}AB^2}[/latex], et [latex]NP[/latex] aequ. [latex]\sqrt{AF^2–\dfrac{1}{4}AC^2}[/latex]. Ergo [latex]AB+\sqrt{AF^2–\dfrac{1}{4}AC^2}:AC\sqrt{AF^2–\dfrac{1}{4}AB^2}::FL:FK[/latex] seu erit [latex]FL[/latex] aequ. [latex]AF\sqrt{AF^2–\dfrac{1}{4}AC^2}\smile\dfrac{1}{2}AB[/latex]. [latex]FK[/latex] aequ. [latex]AF\sqrt{AF^2–\dfrac{1}{4}AB^2}\smile\dfrac{1}{2}AC[/latex]. Et supra [latex]KL[/latex] aequ. [latex]\dfrac{2BC.AF^2}{AB.AC}[/latex].

[On the side:] [latex]\dfrac{KL}{AL} \sqcap \dfrac{BC}{AB}[/latex] [End]

Trianguli autem [latex]FKL[/latex] idem est angulus ad [latex]F[/latex] qui est angulus sphaericus [latex]BAC[/latex]. Eodem modo et caeteros angulos sphaericos in plano poterimus exhibere uti iam ipsa latera Trianguli sphaerici in plano exhibuimus per suas chordas. Et omnia haec triangula consistent circa idem punctum [latex]F[/latex].

[At the end:]

[latex]KL\sqcap \dfrac{BC(AL)AF^2}{AB\dfrac{1}{2}AC}[/latex] [latex]KL\sqcap \dfrac{2BC.AF^2}{AB.AC}[/latex]

[End]

Trigonometria sphaerica projectione in planum explicata

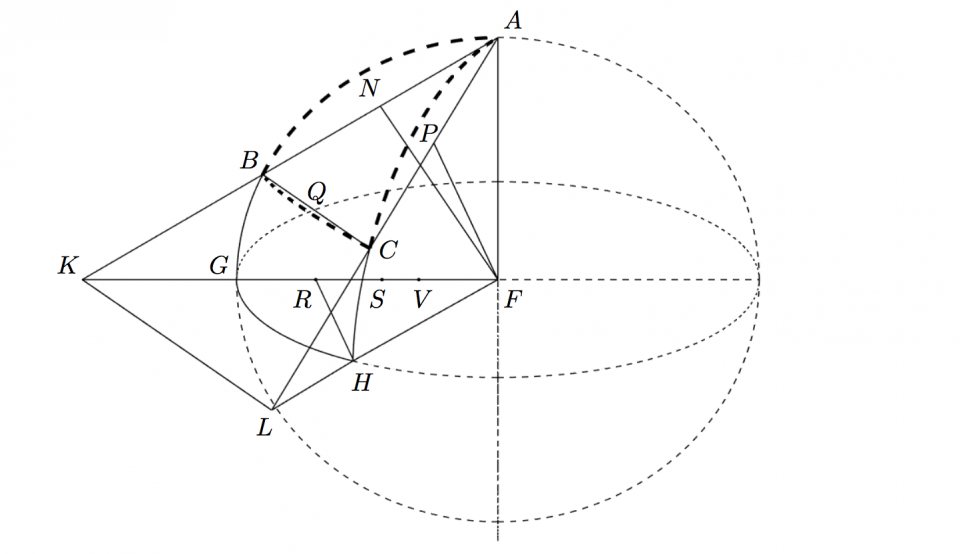
In Sphaera centro [latex]F[/latex], radio [latex]FA[/latex] descripta, sit Triangulum Sphaericum (ex arcubus circulorum maximorum constans) [latex]ABC[/latex] polo [latex]A[/latex], meridianorum quadrantibus [latex]ABG, ACH[/latex] describatur arcus aequatoris [latex]GH[/latex]. Et ducantur radii [latex]FG, FH[/latex] aequales ipsi [latex]FA[/latex], et ad [latex]AF[/latex] normales. Habemus duos quadrantes planos [latex]ABGF[/latex] et [latex]ACHF[/latex], quorum angulus est idem qui rectarum [latex]GF, HF[/latex], unde arcus aequatoris [latex]GH[/latex] erit mensura anguli duorum planorum, seu anguli sphaerici [latex]A[/latex].

Jungantur puncta [latex]A. B. C.[/latex] rectis, et habebitur Triangulum rectilineum [latex]ABC[/latex] quod erit communis sectio sphaerae, et plani per tria puncta [latex]A. B. C.[/latex] transeuntis. Cum rectae [latex]AB, FG[/latex] sint in eodem plano, sunt enim ambae in quadrante plano [latex]ABGF[/latex], productae convenient alicubi in puncto [latex]K[/latex] (parallelae enim non sunt, quia angulus [latex]AB[/latex] ad [latex]AF[/latex] acutus, [latex]GF[/latex] ad [latex]AF[/latex] rectus) similiter [latex]AC[/latex] et [latex]FH[/latex], cum sint in eodem plano, nempe in quadrante plano [latex]ACHF[/latex], convenient alicubi in [latex]L[/latex]. In recta [latex]AB[/latex] sumatur punctum medium [latex]N[/latex], et in [latex]AC[/latex] medium [latex]P[/latex], et jungantur [latex]FN, FP[/latex], erunt anguli [latex]N[/latex] et [latex]P[/latex] recti. Ergo triangula rectangula similia [latex]ANF[/latex] et [latex]AFK[/latex], item similia [latex]APF[/latex] et [latex]AFL[/latex]. Ergo [latex]AN : AF : NF :: AF : AK : FK[/latex]. Similiter [latex]AP : AF : PF :: AF : AL : FL[/latex]. Ergo [latex]AF[/latex] media proportionalis inter [latex]AN[/latex] et [latex]AK[/latex], item inter [latex]AP[/latex] et [latex]AL[/latex]. Ergo rectangulum [latex]NAK[/latex] aequale rectangulo [latex]PAL[/latex], ac proinde et rectangulum [latex]BAK[/latex] aequale rectangulo [latex]CAL[/latex]. Ergo [latex]AB : AC :: AL : AK[/latex]. Triangula ergo [latex]ABC, ALK[/latex] angulum [latex]A[/latex] communem habentia, et latera angulum [latex]A[/latex], comprehendentia, proportionalia; erunt similia, et quod notabile subcontraria.

Ex his si valores linearum rectarum quaeramus, erit [latex]AK[/latex] aequ. [latex]AF^2\smile AN[/latex] et [latex]AL[/latex] aequ. [latex]AF^2\smile AP[/latex] et [latex]KL[/latex] aequ. [latex]BC.AL\smile AB[/latex] vel quia [latex]BQ[/latex] est [latex]\dfrac{1}{2}BC[/latex], et [latex]AN[/latex] est [latex]\dfrac{1}{2}AB[/latex], erit [latex]KL[/latex] aequ. [latex]BQ.Al\smile AN[/latex] et pro [latex]AL[/latex] substituendo valorem [latex]AF^2\smile AP[/latex] fiet [latex]\underline{\underline{KL}}[/latex] aequ. [latex]BQ.AF^2\smile \overline{AP.AN}[/latex]. Seu [latex]KL[/latex] ad sinum ipsius arcus [latex]BC[/latex], (Lateris Trianguli sphaerici) ut in composita ratione sinus totius ad sinus reliquorum laterum. [latex]KF^2[/latex] aequ. [latex]KF^2-AF^2[/latex]. Ergo [latex]KF^2[/latex] aequ. [latex]AF^4-AF^2.AN^2[/latex], [latex]\smile AN^2[/latex] seu [latex]KF[/latex] aequ. [latex]AF\sqrt{AF^2-AN^2}\smile AN[/latex]. et [latex]LF^2[/latex] aequ. [latex]AL^2-AF^2[/latex]. Ergo [latex]LF^2[/latex] aequ. [latex]AF^4-AF^2. AP^2[/latex], [latex]\smile AP^2[/latex] ergo erit [latex]LF[/latex] aequ. [latex]AF\sqrt{AF^2-AP^2}\smile AP[/latex]. [latex]\sqrt{AF^2-AN^2}[/latex] est [latex]FN[/latex]. et [latex]{AF^2-AP^2}[/latex] est [latex]FP[/latex]. Unde [latex]\underline{\underline{KF}}[/latex] aequ. [latex]AF.FN\smile AN[/latex] et [latex]\underline{\underline{LF}}[/latex] aequ. [latex]AF.FP\smile AP[/latex]. Unde valores [latex]KL.KF.LF[/latex] conjungendo fiet: [latex]LF.FK\smile LK[/latex] aequ. [latex]FN.FP\smile BQ[/latex]. Quae theoremata omnia sunt elegantissima.

Et dato Triangulo [latex]ABC[/latex] plano, seu sinibus laterum Trianguli sphaerici potest construi triangulum planum [latex]FKL[/latex] habens angulum [latex]F[/latex] eundem cum angulo trianguli sphaerici [latex]A[/latex]. Idemque est de caeteris angulis sphaericis. Unde datis omnibus lateribus trianguli sphaerici habentur et anguli. Quae calculo prosequi operae pretium erit. Si jam addatur alibi a nobis aliisque demonstratum sinus laterum et sinus angulorum oppositorum esse proportionales cuncta eo facilius absolventur. Datis autem tribus lateribus: [latex]FL, FK, LK[/latex]. angulus F ex communi Trigonometria ita invenitur: fiat ut duplum rectang. [latex]FL.FK[/latex] ad differentiam inter [latex]FK^2+FL^2[/latex] et [latex]LK^2[/latex] ita sinus totus [latex]AF[/latex] ad [latex]FR[/latex] ad sinum complementi anguli [latex]GFH[/latex]. ([latex]R[/latex] autem rectus intelligi debet.) Per supra dicta [latex]LF.FK[/latex] aequ. [latex]FN.FP.LK\smile BQ[/latex]. Et [latex]LK\smile BK[/latex] aequ. [latex]AF^2\smile AP.AN[/latex]. Ergo [latex]LF.FK[/latex] aequ. [latex]FN.FP.AF^2\smile AP.AN[/latex]. [latex]\pm FK^2\pm FL^2\pm LK^2[/latex] aequ. [latex]\pm AF^2.FN^2\smile AN^2[/latex], [latex]\pm AF^2. FP^2\smile AP^2[/latex], [latex]\pm BQ^2.AF^4\smile AN^2.AP^2[/latex], seu aequ. [latex]\pm AF^2.FN^2.AP^2\pm AF^2.FP^2.AN^2\pm BQ^2.AF^4, \smile AN^2.AP^2[/latex]. Sit sinus Totus [latex]FT[/latex]. eritque [latex]FR : FT :: \pm FN^2.AP2\pm FP^2.AN2\pm FT^2.BQ2 : 2, FN.FP.AP.AN[/latex]. Seu [latex]FR\smile FT[/latex] aequ. [latex]\pm\dfrac{1}{2}.\pm\dfrac{FN.AP}{FP.AN}\pm\dfrac{1}{2} \dfrac{FP.AN}{FN.AP}\pm\dfrac{1}{2} \dfrac{FT^2.BQ^2}{FN.FP.AP.AN}[/latex]. Sint
[latex]FR.FS.FV[/latex] sinus compl. angulorum [latex]A. B. C.[/latex] Pro [latex]FS[/latex] loco [latex]A. B. N. P. C. Q[/latex] ponetur [latex]B. A. N. Q. C. P[/latex]. Pro [latex]FT[/latex] loco [latex]A. B. N. P. C. Q[/latex] ponetur [latex]C. A. P. Q. B. N.[/latex] Ergo [latex]FS\smile FT[/latex] aequ. [latex]:: \pm FN^2.BQ^2\pm FQ^2.BN^2\pm FT^2.AP : 2, FN.FQ.BQ.BN[/latex]. Et [latex]FV\smile FT[/latex] aequ. [latex]:: \pm FP^2.CQ^2+/-FQ^2.CP^2\pm FT^2.AN^2 : 2, FP.FQ.CQ.CP[/latex].

Sunt autem [latex]AN[/latex] et [latex]BN[/latex], item [latex]AP[/latex] et [latex]CP[/latex], item [latex]CQ[/latex] et [latex]BQ[/latex] aequales. Sinus scilicet recti arcuum [latex]AB, AC, BC, FN, FP; FQ[/latex] sicut sinus complementi eorundem arcuum. Sinum rectum vel sinum compl. arcus [latex]AB[/latex]. scribemus [latex]SrAB. ScAB[/latex] et sinum complementi anguli [latex]A[/latex], scribemus:[latex] ScA[/latex]. et ita valores ipsorum [latex]FR. FS. FV[/latex]. Seu [latex]ScA. ScB. ScC[/latex] denuo scribemus

[latex]\dfrac{2ScA}{rad}[/latex] aequ. [latex]\pm\dfrac{ScAB}{SrAB}.\dfrac{SrAC}{ScAC}\pm\dfrac{ScAC}{SrAC}.\dfrac{SrAB}{ScAB} \pm\dfrac{rad^2.\overline{SrBC^2}}{SrAB.ScAB.SrAC.ScAC}[/latex]

[latex]\dfrac{2ScB}{rad}[/latex] aequ. [latex]\pm\dfrac{ScAB}{SrAB}.\dfrac{SrBC}{ScBC}\pm\dfrac{ScBC}{SrBC}.\dfrac{SrAB}{ScAB}\pm \dfrac{rad^2.\overline{SrAC}}{SrAB.ScAB.SrBC.ScBC}[/latex]

[On the side:]

[latex]Sc.[/latex] sinus compl. Anguli [latex]A[/latex]

[latex]Sc.AB[/latex] sinus compl. Arcus [latex]AB[/latex]

[latex]Sr.AB[/latex] sinus rectus Arcus [latex]AB[/latex]

Radius. rad

[End]