De Angulis Linearum plane nova (26 Maji 1683)

Transcription of De Angulis Linearum plane nova (26 Maji 1683)

[In the margin, on the top] Hoc schediasmate satis rem plane et compendiose complexus sum.

Curvarum linearum naturam nondum satis explicatam haberi indicio est, quod nondum regula habetur ex qua cognoscatur an duo arcus sibi occurrentes, angulum faciant, an vero unam curvam componant.

Neque enim unitas curvae sumi potest ex uniformitate generationis, nam possunt excogitari motus eandem semper legem servantes, in quibus punctum aliquod describens duarum diversum curvarum arcus successive efficit angulumque suo motu facit.

Item neque etiam ex solis tangentibus dijudicari potest quaestio, quasi eae curvae ut [latex]AB, EB[/latex] pro una continuata [latex]AB[/latex] haberi debeant, quarum tangentes angulum non faciunt; Id enim non sufficere ex eo patet, quo duae curvae se tangentes [latex]ABC[/latex], [latex]DBE[/latex] habent rectam tangentem communem. Et ideo tangentes arcuum [latex]AB[/latex] et [latex]EB[/latex] nempe rectae [latex]FB[/latex] et [latex]GB[/latex] nullum faciunt angulum, et tamen arcus isti [latex]ABBE[/latex] non componunt unam curvam sed angulum [latex]ABE[/latex] aliquem sane licet minime comparabilem cum angulo duarum rectarum, qui dicitur angulus contactus.

Sciendum est autem angulos curvarum habere infinitos gradus, ut nunc ostendam, et dari angulum quem voco osculi, qui est ad angulum contactus, ut angulus contactus ad rectilineum. Et curvae quae sese osculantur in puncto osculi habent non tantum eandem directionem, ut eae quae sese simpliciter tangunt sed et eandem flexionem seu primam directionis mutationem nec faciunt angulum contactus comparabilem cum Angulo contactus circulorum, et tamen eandem lineam non componunt.

Sunt enim tres occursuum gradus: Nodus, contactus et osculum. Nodus cum curva curvam attingit, seu cum habent punctum commune. Contactus cum in puncto communi eandem habent directionem seu rectam tangentem sive arctissime stringentem, recta enim tangens non nisi una est. Osculum cum in puncto contactus eandem habent flexionem seu eundem circulum arctissime stringentem sive omnium intus tangentium circulorum maximum. Osculi autem ipsis rursum gradus sunt infiniti, et quae eandem habent circulum arctissime stringentem, possunt diversas habere Ellipses arctissime stringentes.

Haec omnia ut distinctius intelligantur considerandum est directionem curvae pendere a duobus punctis in ea sumtis [latex]C[/latex] et [latex]D[/latex] intervallo infinite parvo dissitis seu coincidentibus, per quae transiens recta est tangens. Finge enim rectam secantem [latex]AB[/latex] tamdiu moveri ex [latex]A1B[/latex] in [latex]A2B[/latex]. [latex]A3B[/latex], donec e curva exeat, manifestum est duo puncta sectionis [latex]C[/latex] et [latex]D[/latex] sibi magis magisque accedere primum [latex]1C[/latex]. [latex]1D[/latex] deinde [latex]1D[/latex]. [latex]2D[/latex] et tandem in contactu coincidere [latex]3C[/latex]. [latex]3D[/latex]. Unde tangens repraesentat inclinationem vel declivitatem quam curva in puncto contactus habet. Considerando enim curvam velut polygonum infinitorum laterum ut si polygonum sit [latex]1C2C3CD[/latex] cujus latera ut [latex]1C2C, 2C3C, 3C3D[/latex], sint numero infinita, quantitate vero sint infinite parva, patet unum tale latus ut [latex]3C3D[/latex] esse portionem tangentis [latex]A3C3D3B[/latex] et latus curvae, ut [latex]3D3C[/latex] productum incidere in [latex]A[/latex] seu esse tangentem.

Verum ad curvam a recta discernendam praeter directionem opus est aliqua flexione seu prima directionis mutatione, vel duarum directionum angulo ad se invicem; ac proinde ut directio duobus tantum indiget curvae punctis coincidentibus; ita flexio indiget minimum tribus curvae punctis, [latex]C. D. E [/latex] indefinite propinquis, seu duobus polygoni infinitanguli curvam repraesentantis lateribus [latex]CD[/latex] et [latex]DE[/latex]. Et quemadmodum directionem determinavimus per rectam tangentem, quia datis duobus punctis datur recta per ea transiens; ita flexionem metiemur circulo per tria puncta [latex]C[/latex]. [latex]D[/latex]. [latex]E[/latex] transeunte, qui semper est determinatus. Et centrum hujus circuli semper est a concava parte curvae; et ut recta transiens per [latex]C. D[/latex] seu tangens est eadem ita et recta arctissime stringens; ita circulus transiens per tria puncta [latex]C[/latex] [latex]D [/latex][latex]E[/latex], est circulus ibi curvam arctissime stringens, quem appello osculantem.

Sed dubitabit aliquis quomodo inveniri queat is circulus, cum tria puncta coincidunt seu distantiam habent inassignabilem sive infinite parvam. Respondeo id fieri eodem modo, quo invenitur recta curvam tangens id est in duobus punctis coincidentibus secans. Ut enim problema quo invenitur punctum Contactus seu quo recta vel alia linea curvam propositam tangit duas habet radices aequales; ita problema quo invenitur punctum in quo circulus (vel alia curva nam rectae hic locus non est) curvam propositam osculatur minimum, tres (imo quatuor) habet radices seu valores aequales. Unde vicissim puncto contactus vel osculi dato inveniri potest recta tangens vel circulus.

Et quidem curvam unam in uno puncto non nisi una (proprie) tangit recta, verum circuli infiniti curvam in quovis puncto tangere possunt, quoniam cum unus tantum sit osculans videamus quomodo a caeteris distinguatur.

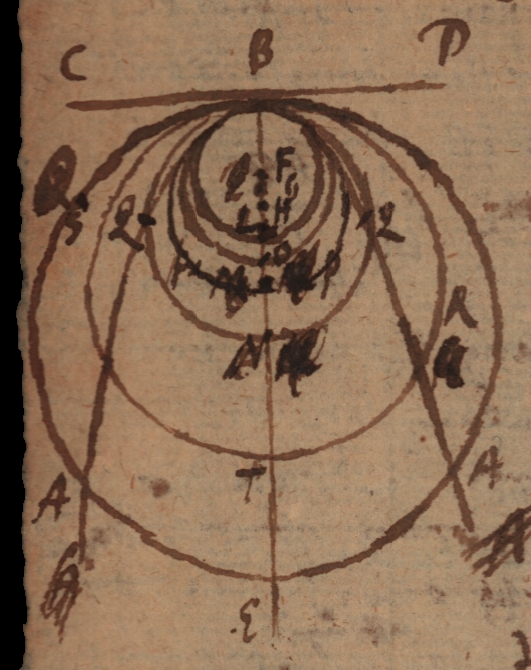
Sit ergo curva [latex]AB[/latex], quam tangat recta [latex]CD[/latex] in [latex]B[/latex] et sit [latex]BE[/latex] ad tangentem perpendicularis ducta intra concavitatem curvae. Manifestum est quemvis circulum centro in hac recta sumto per [latex]B[/latex] descriptum tangere curvam in [latex]B[/latex]. Ex his circulis tangentibus quidam minores cadunt intra curvam, ut descripti centris [latex]F[/latex]. [latex]G[/latex]. [latex]H[/latex], alii vero majores descripti centris [latex]L[/latex]. [latex]M[/latex]. [latex]N[/latex], statim post contactum cadunt extra curvam. Necesse est ergo dari quendam omnium intra curvam cadentium seu in concavo tangentium maximum seu ultimum, qualis sit descriptus centro [latex]H[/latex] radio [latex]BH[/latex], cujus radius si vel tantillum augeretur, ut si pro [latex]BH[/latex] sumeretur [latex]BL[/latex], statim circulus caderet extra curvam, seu a parte convexa tangeret isque circulus curvam arctissimum stringet, quia nullus alius circulus ibidem tangens inter ipsum et curvam poterit describi. Et quidem si ponatur [latex]AB[/latex] esse sectio conica quaecunque cujus vertex sit [latex]B[/latex], erit [latex]HB[/latex] dimidium latus rectum, seu, quod memorabile satis theorema est, in omni sectione conica circulus circa latus rectum descriptus est omnium curvam in vertice intus seu a concava parte tangentium maximus, vel quod eodem redit eandem cum ipsa flexionem habet, sive ipsam in vertice osculatur et, si alius tantillo major assumatur, is extra conicam curvam cadet. Manifestum est etiam, circulum illum osculantem inter omnes circulos tangentes maxime ad curvam quam osculatur accedere, et licet revera non nisi in uno puncto congruere possit, tamen longissimo tractu cum curva congruere videri, et ab ea difficillime discerni posse. Porro si paululum augeatur radius, tunc circulus cadens extra curvam utcunque vicinus osculanti, necessario (nisi punctum [latex]B[/latex] sit ipsum punctum flexus curvae, ubi etiam recta tangens curvam in tribus punctis coincidentibus secat) curvam praeter punctum contactus [latex]B[/latex] adhuc in aliis duobus punctis [latex]Q[/latex]. [latex]Q[/latex] secabit quae puncta [latex]Q[/latex]. [latex]Q[/latex] in circulo osculante coincidunt cum puncto osculi [latex]B[/latex]. Et ita circulus osculans curvam secare intelligendus est in quatuor punctis coincidentibus, nempe in duobus eo ipso quia est tangens, quemadmodum caeteri circuli tangentes omnes; et adhuc in duobus [latex]Q[/latex]. [latex]Q [/latex] qui in casu osculi inter se, et cum contactus punctis coincidunt.

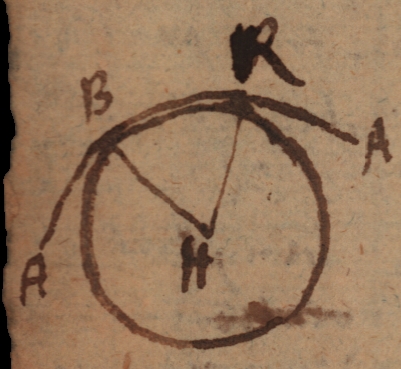
Unde etiam centrum [latex]H[/latex] circuli curvam in puncto dato [latex]B[/latex] osculantis quaerere, idem est ac quaerere centrum circuli curvam tangentis tam in puncto dato [latex]B[/latex], quam in puncto adhuc alio, [latex]R[/latex], sed priori [latex]B[/latex] coincidente; seu quaerere concursum duarum rectarum [latex]BH[/latex], [latex]RH[/latex], curvam [latex]ABR[/latex] in punctis [latex]B[/latex] et [latex]R[/latex] coincidentibus seu infinite parvo intervallo dissitis, ad angulos rectos secantium.
 

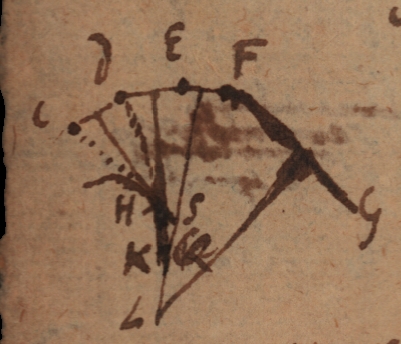
Et licet regulariter non sit in potestate circulum invenire qui transeat per quatuor puncta, [latex]C[/latex]. [latex]D[/latex]. [latex]E[/latex]. [latex]F[/latex], si scilicet perpendiculares ad [latex]CD[/latex] et [latex]DE[/latex] (ex punctis mediis eductae) coincidant in [latex]H[/latex], at ex mediis [latex]DE[/latex] et [latex]EF[/latex] eductae coincidant in [latex]K[/latex]. Hoc loco tamen sufficit nos quaerere concursum perpendicularium ad [latex]CD[/latex] et [latex]EF[/latex], in [latex]S[/latex], ut circulus centro [latex]S[/latex] radio [latex]SC[/latex] descriptus transeat per puncta [latex]C[/latex]. [latex]D[/latex]. [latex]E[/latex]. [latex]F[/latex], nam [latex]SC[/latex], et [latex]SD[/latex] inter se aequales sunt ex constructione, item [latex]SE[/latex] et [latex]SF[/latex] inter se; at [latex]SD[/latex] et [latex]SE[/latex], aequales sunt ex natura casus hujus specialis, quia intervallum inter [latex]D[/latex] et [latex]E[/latex] est inassignabile sive infinite parvum. Unde fit ut problema etsi tres tantum radices aequales prima fronte habere videatur, revera tamen deprehendatur habere radices quatuor. Et, si circulus minor osculante curvae alibi quam in contactu non occurrat, necesse est duas radices, pro punctis [latex]Q[/latex] et [latex]Q[/latex] esse impossibiles. Manifestum est denique si curvae [latex]CDEFG[/latex] quam polygoni infinitanguli instar consideramus, perpendiculares (ex mediis lateribus [latex]CD[/latex]. [latex]DE[/latex]. [latex]EF[/latex]. [latex]FG.[/latex] etc. eductae) intelligantur ordine concurrere (quaevis cum vicina in punctis [latex]H[/latex].[latex]K[/latex]. [latex]L[/latex] etc.) puncta ista concursuum incidere in novam curvam [latex]HKL[/latex], et quidem perpendiculares curvae [latex]CDEF[/latex] fore tangentes curvae [latex]HKL[/latex], et si filum [latex]CHKL[/latex] a [latex]C[/latex] ad [latex]H[/latex] recta extensum, et deinde curvae [latex]HKL[/latex] circumligatum, evolvatur, seu continue tensum moveatur ex [latex]CHKL[/latex] in [latex]DHKL[/latex] ex [latex]DHKL[/latex] in [latex]EKL[/latex] ex [latex]EK[/latex] in [latex]FKL[/latex], ex [latex]FL[/latex] in [latex]GL[/latex] etc. (quem evolvendi modum uberius explicuit clarissimus pendulorum horologiorum inventor) tunc punctum [latex]C[/latex] ordine incidet in puncta [latex]DEFG[/latex], et ita evolutione curvae [latex]HKL[/latex], describetur curva [latex]CDEF[/latex] et curva quae evolutione sui generat aliam curvam, est locus centrorum omnium circulorum curvam generatam osculantium, seu flexiones ejus ordinatim metientium.

Ex his etiam patet non omnem circulum intra curvam aliquam propositam provolvi posse, sed eum demum qui non est major minimo circulo osculante. Ita in parabola concava nullus circulus ubique provolvi potest, nisi sit aequalis aut minor eo cujus diameter est latus rectum. Et memini me hac occasione, cum trochoeides considerarem, quae circulis intra curvas provolutis generantur, in has cogitationes primum incidisse.

Cum ergo circuli aliarum linearum flexiones commodissime metiantur, ut rectae metiuntur directiones, (sunt enim hae duae lineae simplicissimae omnium, et ubique uniformes) consequens est, ut quemadmodum curvarum se se secantium seu in concursu diversas directiones habentium angulos sectionis metimur, angulis rectilineis rectarum tangentium; ita curvarum se tangentium, seu easdem directiones habentium angulos contactus seu flexionis metiamur angulis circularibus circulorum osculantium. Et quemadmodum angulus contactus rectae ad curvam quam tangit vel duarum curvarum tangentium inter se, habetur pro nullo vel infinite parvo respectu anguli vulgaris seu rectilinei, quia est quovis angulo rectlineo minor: ita angulus osculi seu circuli ad curvam quam osculatur habetur pro nullo respectu anguli contactus vulgaris seu circularis, cum sit quovis angulo contactus duorum circulorum, minor. Sic angulus contactus parabolico-circularis [latex]SBA[/latex] quem circulus [latex]BSE[/latex] parabolam in vertice [latex]B[/latex] tangens, cum ipsa parabola [latex]AB[/latex] facit, aequalis censetur angulo contactus circulari [latex]SBP[/latex], quem facit circulus [latex]BSE[/latex], cum circulo [latex]BPM[/latex] parabolam in vertice osculante, cujus diameter est latus rectum.

Nam si alius circulus quilibet loco circuli osculantis assumatur, poterit semper alius assumi parabolae propior; sed inter solum circulum osculantem et curvam alius circulus describi non potest; prorsus quemadmodum inter rectam tangentem et curvam alia recta duci non potest. Et proinde angulus osculi est minor quovis angulo contactus circulari et proinde minor etiam quovis angulo contactus duarum aliarum curvarum se non osculantium. Circulos autem duos sese osculari tam impossibile est, quam duas rectas se tangere nisi coincidant.

Quemadmodum autem circulus ex puncto curvae generatricis tanquam centro, per punctum correspondens curvae evolutione prioris generatae descriptus curvam generatam ibi osculatur, ita etiam Ellipsis ex punctis duarum curva[ru]m congeneratricium tanquam focis per punctum respondens curvae coevolutione priorum generatae descriptus ibi curvam generatam osculatur, ita ut nullus circulus inter hanc Ellipsin et curvam tangendo cadere possit.

Ipsos angulos contactus circulorum ultra metiri nihil necesse est, sufficit enim eos determinatos ese per radios circulorum, si quis tamen curiosius ista scrutari volet haec reperiet: primum, contactum duorum circulorum per omnia similem esse contactui duorum aliorum circulorum eandem inter se rationem habentium. Exempli causa sit [latex]BM[/latex] ad [latex]BN[/latex] ut [latex]BT[/latex] ad [latex]BE[/latex], omnia utrobique similiter seu proportione intelligi posse necesse est. Hinc si sint quatuor diametri circulorum continue proportionales [latex]BM[/latex]. [latex]BN[/latex]. [latex]BT[/latex]. [latex]BE[/latex] erunt tres anguli contactus circulares etiam continue proportionales, [latex]PBQ[/latex]. [latex]QBR[/latex]. [latex]RBA.[/latex] Ergo si tres isti anguli contactus continue sibi appositi essent aequales, forent diametri quatuor continue proportionales; et sumendo angulos contactuum cum circulo primo,[latex]PBQ, PBR, PBA[/latex] etc. progressionis Arithmeticae; forent diametri [latex]BM, BN, BT, BE[/latex] progressionis geometricae, et proinde si diametri crescerent aequabiliter seu ut numeri, progressione arithmetica, tunc anguli contactuum crescent ut Logarithmi. Unde cum recta ipsa haberi possit pro circulo cujus diameter est infinita, sequitur angulum contactus quem facit recta cum circulo esse ad angulum contactus duorum circulorum, ut logarithmus numeri infiniti, ad logarithmum numeri finiti. Caeterum posito logarithmum unitatis esse 0. logarithmus infiniti est quantitas infinita, non quidem absoluta, qualis est ipsum infinitum, cujus est logarithmus, sed media quadam proportione inter finitum et infinitum. Nam si Numerus infinitus ponatur esse: [latex]1+1+1+1[/latex] etc. in infinitum, logarithmus ejus erit [latex]\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}[/latex] etc. in infinitum ut alibi ostensum est. Et proinde si angulus rectilineus ponatur esse [latex]1+1+1+1+1[/latex] etc. erit angulus contactus rectilineo-circularis ut [latex]\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}[/latex] etc. et angulus contactus circularis ut numerus finitus.

Prorsus ut in Tabula Trianguli Harmonici ubi

[latex]\begin{array}{rrrrrrrrrrr} 1&&\frac{1}{1}&&\frac{1}{1}&&\frac{1}{1}&&\frac{1}{1}&&s \\ 1&&\frac{1}{2}&&\frac{1}{3}&&\frac{1}{4}&&\frac{1}{5}&&e \\ 1&&\frac{1}{3}&&\frac{1}{6}&&\frac{1}{10}&&\frac{1}{25}&&r \\ 1&&\frac{1}{4}&&\frac{1}{10}&&\frac{1}{20}&&\frac{1}{35}&&i \\ 1&&\frac{1}{5}&&\frac{1}{15}&&\frac{1}{35}&&\frac{1}{70}&&e \\ {\textrm{etc.}}&&{\textrm{etc.}}&&{\textrm{etc.}}&&{\textrm{etc.}}&&{\textrm{etc.}}&& s \\ \hline {\textrm{infinitum}}&&\frac{1}{0}&&\frac{2}{1}&&\frac{3}{2}&&\frac{4}{3}&&{\textrm{summae}} \end{array}[/latex]

Quae animi gratia adjicere placuit. Ut his probe consideratis controversiae inter Geometras de hoc argumento non sine scientiae opprobrio agitatae finiantur. Nam si metaphysico rigore loqui vellemus, perinde imaginaria sunt talia ut numerus infinitus ac quantitates infinite parvae, et radices impossibiles [latex]\sqrt[2]{-1}[/latex], et focus alter parabolae infinito hinc distans intervallo, quae tamen omnia tanquam instrumenta inveniendi merito recipiuntur, quoniam quae inde deducuntur demonstrari possunt reductione ad absurdum.

Sed redeamus in viam, et quoniam ad angulos osculi pervenimus, eosque non possumus metiri contactibus circulorum, (quemadmodum angulos contactuum non poteramus metiri sectionibus rectarum) progrediendum est ad alias curvas altiores, licet nullae occurrant uniformes.

Annotavimus supra Circuli qui sectionem conicam in vertice osculatur, diametrum esse latus rectum. Itaque duae sectiones conicae, quae idem habent latus rectum ita positae ut convexitas unius tangat concavitatem alterius in vertice communi, sese osculabuntur, id est nullus describi poterit circulus eas in vertice tangens, qui inter ipsas cadat. Hunc ergo angulum osculi ut metiamur poterimus uti Ellipsi eodem modo ut antea usi sumus circulo.

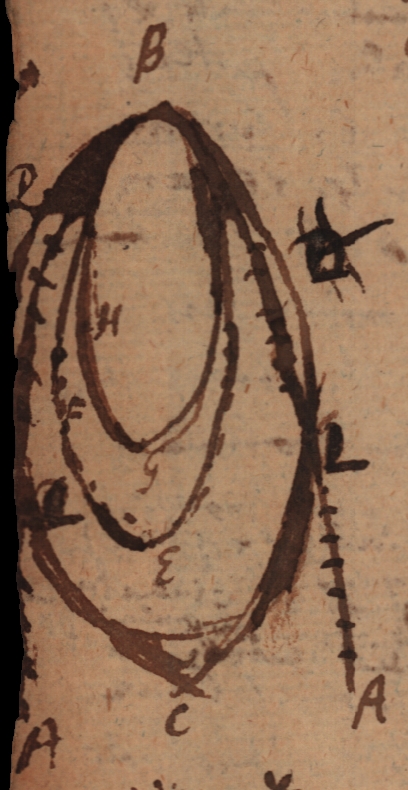
Sit sectio conica velut parabola [latex]ABA[/latex], ejus verticem verticibus suis osculari possunt Ellipses innumerae [latex]HBG, FBE, LBC[/latex]; omnes scilicet quae idem habent latus rectum cum proposita sectione cum tamen non congruant inter se, ideo quaedam Ellipsium osculantium statim post osculum cadent extra curvam ut [latex]CDB[/latex], quaedam intra ut [latex]GHB[/latex]. Sed omnium intra curvam cadentium Ellipsium erit quaedam maxima [latex]EFB[/latex], quae si vel tantillum (manente latere recto) augeretur statim (salvo licet osculo) extra caderet, eaque intus cadentium maxima, quae sit [latex]EFB[/latex] tam arcte curvam [latex]AB[/latex] stringet, ut nulla Ellipsis (osculans) inter ipsam et curvam describi possit. Et haec Ellipsis secundum curvedinis gradum, seu ipsam mutationem flexionis metietur, perinde ac Circulus supra primum curvedinis gradum seu mutationem directionis id est flexionem metiebatur. Et quemadmodum ad directionem curvae cognoscendam duo, et ad flexionem tria puncta inassignabiliter distantia (seu coincidentia) unum aliquid efficientia adhibentur. Ita ad flexionem flexionis, seu secundum curvedinis gradum minimum requiruntur puncta quatuor, coincidentia.

Et quemadmodum problema invenire punctum arctissimi contactus, seu punctum osculi; est ad minimum trium, revera quatuor radicum aequalium, ita inveniri punctum arctissimi osculi, seu punctum strictionis est minimum quatuor imo sex radicum aequalium. Unde vicissim Ellipseos stringentis foci inveniri poterunt. Vel latus transversum (ob datum jam rectum) inveniri poterit, quod magnitudine sua ipsum osculi arctitudinem, seu secundum curvedinis gradum definit.

Sex autem revera radices aequales fiunt, quia Ellipsis [latex]CDB[/latex] eo ipso quia osculatur, secat in quatuor punctis coincidentibus per superiora; at eadem si extra osculatur, secat adhuc in duobus, [latex]L[/latex]. [latex]L[/latex]. quae in Ellipsi stringente [latex]EFB[/latex] coeunt in punctum [latex]B[/latex]. Ergo in [latex]B[/latex] sunt sex puncta coincidentia, vel poni potest curvam ab Ellipsi ter tangi tribusve tactuum punctis coincidentibus.

Eodem modo si duae curvae ne ullum quidem angulum osculi (primi gradus) facerent, sive si eandem haberent Ellipsin stringentem hoc est arctissime osculantem; nihilo minus quia non congruerent sed angulum novum facerent infinities licet minorem angulo osculi, ascendendum esset ad tertium curvedinis, sive secundum angulorum osculi gradum adhibitis curvis altioribus, quae in octo punctis coincidentibus curvae occurrere possint. Atque ita in infinitum. Et tum demum curva curvam continuare. Hoc est nullum cum ea angulum ullius gradus facere sed unam lineam componere intelligetur; cum in puncto communi eadem semper curva osculans quotcunque assumtis [latex]\langle[/latex]pu[latex]\rangle[/latex]nctis coincidentibus reperietur.

Tantum