Angles of contact
In 1686, Leibniz published “Meditatio nova de natura anguli contactus et osculi” (Leibniz, 1686). This article is the fruit of investigations conducted in the previous years in order to resolve new geometrical and optics problems, concerning the characterization of contacts between two curves. To do so, Leibniz revisited the figure of the angle of contact – that is to say the angle between a circle, or more generally a curve, and one of its tangents – figure which had provoked many discussions during the Renaissance specially between Christoph Clavius and Jacques Pelletier. In order to characterize different degrees of contact between two curves, Leibniz generalized the notion of angle of contact in an original way by introducing the idea of angles of osculation — namely, angles which follow each other by degrees of infinity, and which are incomparable from one degree to another.
This section presents several texts – dating from 1681 to 1686 – containing research that was either successful or not, but which led to the results published in the article Meditatio. Leibniz’s investigations about angles of contact emerged in a context in which he also questioned the foundations of geometry and thought on new grounds basic geometrical notions – such as homogeneity, similarity and measure – (De Risi, 2007), (Leibniz 2018). One of the main interests of these texts is that, perhaps as a way of legitimising his geometrical reformulations, Leibniz tested his new notions of angle of contact and angles and osculation by means of the former to see if they can be considered as magnitudes, and whether they can be measured directly – as in the case of magnitudes consisting partes extra partes which are measured by a common measure – or indirectly – as in the case of rectilinear angles, which are measured as the ratio of the arc to the lengh of the circumference –. His attempts are particularly noteworthy in “De Angulus Linearum plane nova” (See here) and “De Angulus Contactus et Curvedine et de natura quantitatis” (See here). Leibniz introduced the osculating circle and tried to characterise it by determining the formula for its radius. Most of these texts show that Leibniz knew the identity between the locus of the centres of the osculating circles of a curve and its evolute, but he did not succeed in finding a general formula for the radius of curvature that would provide a measure of the angle between two tangent curves. Jacques Bernoulli's manuscripts show that he knew the formulas at least as early as 1691, and he published them in 1694 (Bernoulli Jacob, 1694), (Radelet-de-Grave, 2004).
Multa et mira de Angulo contactus
Overview of Multa et mira de Angulo contactus
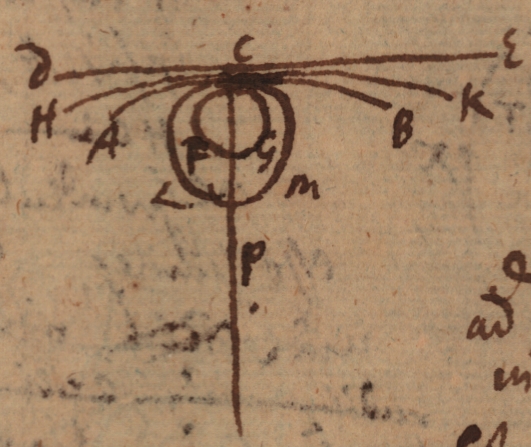
Leibniz wrote this manuscript on December 3/13, 1681. As far as we know, this is the first manuscript in which he explains how he found "a clear measure of the angle of contact".
According to Leibniz, the angle of contact between a curve and its tangent is measured by the curvature, which is itself measured by a circle. But why? Leibniz claims that the circle is the only plane figure that has the same angle of contact with either of its tangents, and this on both sides of the tangent - which is not the case, he stressed, for the other curves. Moreover, because all circles are similar and their curvature is produced similarly, it follows that - sunt effectus in ratione causarum - their curvatures are like their radii.
To measure the angle of contact at any point of a curve, Leibniz then reasons by analogy. In the same way that the tangent measures the direction because it is the straight line that extends from each side of the curve to the side of the convexity - which corresponds to two equal roots -, the largest of the tangent circles inside the concavity of the curve will be the circle that gives the curvature. In this case, the problem corresponds to - Leibniz emphasizes - at least three equal roots.
However, for Leibniz, who based his reasoning mainly on diagrammatic considerations, it is not clear whether the circle measuring the curvature - Leibniz has not yet called it "osculator" - should remain strictly within the concavity of the curve before and after the contact. In almost all points of a curve the osculating circle touches the curve by crossing it - which corresponds to exactly three equal roots - but in the case of certain vertices - that of the parabola or other conics - on which Leibniz precisely focuses his investigation here and in other of these manuscripts - "De Angulis Curvarum" and “De Angulis Linearum plane nova" - the circle remains inside the curve and the problem corresponds to four equal roots. Later, Leibniz will insist on making this particular case the general case, ad that, until Johann Bernoulli persuaded him to the contrary in 1695.
Even if the method for determining the circle of curvature was not yet established, the introduction of this concept lead Leibniz to make sense of the angle of contact between a curve and its tangent: it is the same as the angle of contact between the circle and the tangent, and is measured by the radius of the circle.
De Angulis Curvarum
Overview of De Angulis Curvarum
"De Angulis Curvarum", as well as "De Angulo contactus et curvedine et de natura quantitatis", was most probably written after 1682 – since the conceptual elaborations on curvature are more advanced than in “Multa et mira de Angulo contactus”, but a little before June 1683 – since we find in "De Angulis Linearum plane nova" a reprise of the issues dealt with in the three manuscripts.
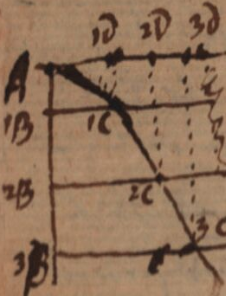
Leibniz introduced the concepts of convexity/concavity and that of the direction of a curve by means of kinematic considerations – considerations that can be found in later writings, such as "Specimen geometriae luciferae" (Gerhardt, GM, VII). The idea is to consider a curve as resulting from a double rectilinear motion: that of a point moving along a straight line, which itself parallel to itself maintaining the same angle with respect to a second given line.
The tangent at a point of the curve is the direction that this point would take, endowed with the resultant of the two velocities, at the moment when their external cause ceases to act. This observation allows Leibniz claims that we can consider that the angle made by two intersecting curves is the same as the rectilinear angle between their two tangents, and that therefore the angle of contact can be considered to be null in respect to the rectilinear angle.
It is only when the two curves are tangent that the comparison of the angles of contact is of any interest, since in this case, Leibniz states that the angle they make is considered to be the same as that made by two particular tangent circles. Each of this pair of circles has the same angle of contact as the respective curve has with its tangent, and consequently – Leibniz claims – it has the same curvature.
As in “Multa et mira de Angulo contactus”, Leibniz seeks the circle of the same curvature by relying on diagrammatic considerations: it is the tangent circle with the greatest radius of all the circles that fall inside the curve and such that if its radius is increased a little, it will fall outside the curve. Here, he also oscillates on the number of roots needed - three or more - to determine the osculating circle (this designation as well as “angle of osculation” is made in the margin of the page).
In “De Angulis Linearum plane nova” and in the article from Acta Eruditorum “Meditatio nova de natura anguli contactus et osculi” (Leibniz, 1686), Leibniz did not present any computation, but formulated what he designated as a "Theorema memorabile": at the vertex of a conic, the radius of the osculating circle is equal to half the latus rectum. In the "De Angulis Curvarum", we find the computations that were necessary for Leibniz to obtain this result. Furthermore, Leibniz also obtained by calculation the equation of the locus of the centers of curvature of the ordinary parabola, which he identified - for the first time, it seems – with the evolute of the curve in this particular case but, more importantly, in the general case.
De Angulis Linearum plane nova
Overview of De Angulis Linearum plane nova
"De Angulis Linearum plane nova" appears to be the result of the research conducted in the three manuscripts "Multa et mira de Angulo contactus" and especially "De Angulis Curvarum" and "De Angulo contactus et curvedine et de natura quantitatis". To begin with, in the top right margin, Leibniz writes that with this scheda he has summarised matters concerning the angles of curved lines in a "complete and clear" manner. Indeed, from the very first lines, he announces that he is intending to show that the angles of the curves - which he immediately names "angles of osculation" - are of any degree, incomparable from one degree to another. To every degree of osculation corresponds a curve of osculation: first the circle followed by "ellipses" of any degree. In the following, he develops most of the questions dealt with in the other three manuscripts, but unlike "De Angulis Curvarum", he does not carry out any computation.
Leibniz continues to characterise the osculation circle as the one which, among tangent circles, is the most 'tightly' connected to the curve and the last [ultimum] to remain strictly in the curve. He also states his "Theorema memorabile": at the vertex of a conic, the radius of the osculating circle is equal to half the latus rectum.
However, he no longer hesitates to state that the osculating circle is obtained not by equality of three roots but of four roots. His insistence on this subject is such that he presents the idea of a method of determination of the circle of osculation considering it as passing through four coincident points of the curve.
This method consists in determining the centre of the circle as the intersection of three pairs of perpendiculars to segments whose extremities are points infinitely close. In fact, this method is a modified version of the method of determining the evolute of a curve, and again testifies to the fact that around 1683, Leibniz was aware of the identity between the locus of the centres of the circles of osculation of a curve and its evolute.
De Angulo contactus et curvedine et de natura quantitatis
Overview of De Angulo contactus et curvedine et de natura quantitatis
Among the texts preceding the “Meditatio nova de natura anguli contactus et osculi” (Leibniz, 1686), the “De angulo contactus et curvedine et de natura quantitatis” holds a special place. Indeed, it is the only text in which Leibniz attempted to legitimise circular angles as magnitudes (on the grounds of his own reformulations of the basic Euclidean concepts, also expressed in other writings from this period). This is significant because in other texts, in particular in the Meditatio, he states that the angle between the two osculating circles of two tangent curves could be used to estimate the angle between these curves. This is made possible thanks to the introduction of the angle of osculation, which Leibniz defined as the angle between the curve and its osculating circle. The angle of osculation is presented as the smallest angle between the curve and one of its tangent circles. It is infinitely small in comparison to the angle of contact.
According to Leibniz, the debate between Pelletier and Clavius did not lead to a consensus because of the lack of a precise notion of what a quantity was. Leibniz distinguishes two approaches in the understanding of quantity. In the first, the condition for a thing to be considered as a quantity is that it can be said lesser or greater because it is contained in or contains the other. This is the sense in which the angle of contact is said smaller than any rectilinear angle. But Leibniz pointed out that this approach is lax because it would be tantamount to saying that the point, since it is contained in the line, is a quantity. In the second approach, stricter [“arctiore”], he considered that for things to be quantities, they must have parts that are homogeneous to the whole. Consequently, to be in (be contained in) a thing is not sufficient to be a part of it. This second approach would not be particularly original if Leibniz did not propose a new definition of homogeneity. He considered that homogeneous things are those which are similar or which can become so by a transformation preserving the magnitude. Leibniz recalled the Euclidean anthyphairesis: to compare two magnitudes one removes the smaller from the greater as many times as possible, then the rest from the smaller, and the second rest from the first, and so on ... the result is either an exact common measure, or a magnitude that can be rendered as small as one wishes so that the error becomes less than any given. In Euclid’s Elements, the existence of a ratio between two magnitudes implies that these magnitudes are yet homogeneous (def. 3 of Book V). Thus, as many of his contemporaries, Leibniz interpreted Euclid's algorithm for determining a common measure as Euclid's definition of homogeneity between magnitudes, even if Euclid never defined the term "homogeneity". Moreover, Leibniz pointed out that his way of defining homogeneity is “simpler” and more general.
Leibniz tested these definitions on rectilinear and circular angles. He introduced a way of measuring circular angles by assuming that when tangent circles have their diameters in geometrical progression, the successive circular angles are equal. This measure enabled him to formulate a “Theorema mirabile” which states a comparison between circular angles, angles of contact and rectilinear angles: a circular angle is to an angle of contact as the logarithm of a finite number is to the logarithm of the infinite number, and an angle of contact is to a rectilinear angle as the logarithm of the infinite number is to the infinite number. Leibniz reproduced this development in De Angulus Linearum plane nova. This theorem seems to contradict the assumption asserted by Leibniz in other texts that circular and rectilinear angles belong to the same degree of infinity, and therefore it conduces to question the validity of the measure of circular angles proposed above.