Transcription of Untitled (Tables sur la formule de Heron)
Folio principal - RECTO -
DE CONDENDA TABULA PRO AREIL TRIANGULORUM EX DATIS LATERIBUS
Martii 1678


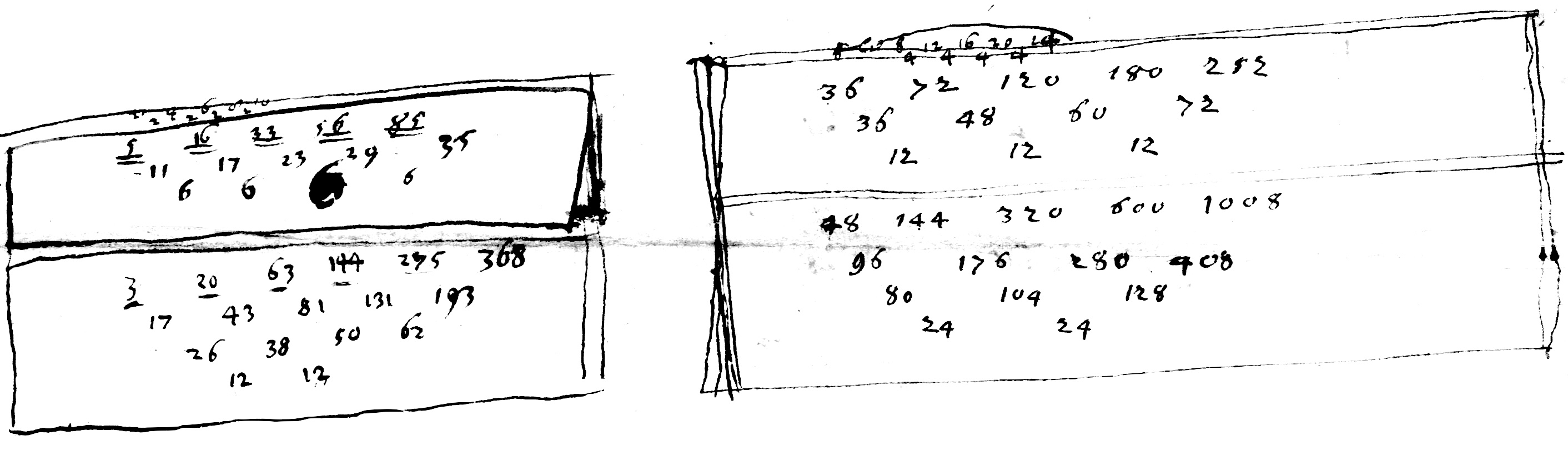
$A$ : numeri ordine combinati item excessus duorum quorumlibet trianguli laterum in B comprehensorum supra tertium.
$B$ : latera omnium Triangulorum in numeris possibilia excessis illis quibusdam, ut $1$.$1$.$1$ vel $1$.$2$.$2$ vel $2$.$3$.$4$ vel $4$.$5$.$6$. Hæc enim duplicentur tantum, et sumantur eorum dupla ut $2$.$2$.$2$ vel $2$.$4$.$4$ vel $4$.$6$.$8$ ita tamen ut areæ trianguli quadratum $E$ ut $3$ vel $15$ vel $135$ postea inventum dividatur per $16$ quotiens erit quadratus areæ trianguli quæsiti.
$C$ : summa ipsorum numerorum sub $A$ vel dimidia summa comprehensorum sub B seu dimidia summa laterum trianguli.
$D$ : productum ex tribus numeris $A$ in se continue ductis. $E$ : productum ex $C$ in $D$ seu quadratum areæ trianguli cuius latera $B$, id est si ex numero
$E$ extrahatur radix quadrata habebitur area trianguli.
$F$ : differentiae quadratorum arearum seu numerorum $E$.
$G$ : differentiae differentiarum, quae semper eadem numeris duobus primis manentibus iisdem
Progressio ipsorum $G$. et primorum terminorum ipsorum $F$ et ipsorum $E$ in quolibet membro in terminis $A$. ejusdem capitis sive Transitus de membro in membrum
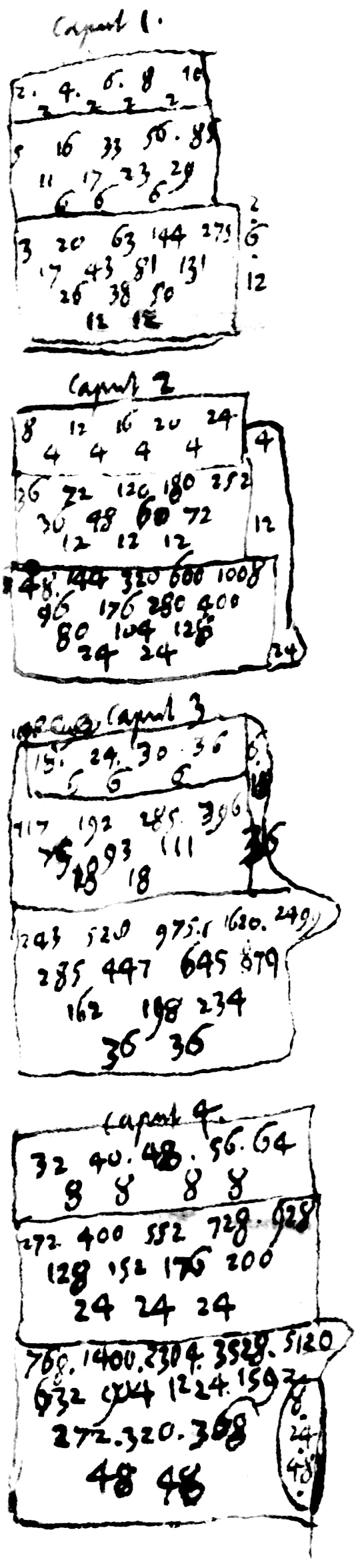
progressio differentiarum transitarum de membro in membrum, sumta de capite in caput.
$\begin{array}{ccc} 2&6&12 \\ 4&12&24 \\ 6&18&36 \\ 8&24&48 \end{array}$
Progressio primorum $G$ . $F$ . $E$ . in quolibet capite, seu transitus seu in terminis $A$ cuiuslibet capitis, sive transitus de capite in caput

$L$ æqu. $4y^3+y^2$. posito $y$ esse primum $A$ capitis $M$ æqu. $3y^4$
$\begin{array}{c|cccccccc} 1&0&0&0&0&0&0&0&0 \\ 2&0&3&0&1&0&3&0&0 \\ 3&0&4&7&7&1&2&1&3 \\ 6&0&7&7&8&1&5&1&3 \\ \hline &1&5&5&6&3&0&2&6 \end{array}$
$\begin{array}{ccccccccc} 2)&0&7&7&8&1&5&1&3 \end{array}$
Optima via est per logarithmos trium numerorum sub $A$ et quarti sub $C$. logarithmi invicem addantur a summa dimidio erit Logarithmus areæ quæsitæ. v.g. si Trianguli latera $3. 4. 5.$ erunt differentiæ $1. 2. 3.$ logarithmi
$\begin{array}{ccccccccc} &0&0&0&0&0&0&0&0 \\ &0&3&0&1&0&3&0&0 \\ &0&4&7&7&1&2&1&3 \\ \hline +&0&7&7&8&1&5&1&3 \end{array}$ $\begin{array}{ccccccccc} &0&7&7&8&1&5&1&3 \\ &&&&&&&&2 \\ \hline +&1&5&5&6&3&0&2&6 \\ -&0&6&0&2&0&6&0&0 \\ \hline &0&9&5&4&2&4&2&6 \end{array}$
Ad progressionem perctam opus quatuor trangulis in quolibet membro. quinque membri in quolibet capite. Et denique sex capitibus pro toto calculo
$\fbox{$\begin{array}{ccccccccccccc} 5&6&6&&11&11&12&&17&&180&&3060 \end{array}$}$
$\begin{array}{ccccccccccccc} 6&7&7&&13&13&14&&20&&294&&5880 \end{array}$
- VERSO -
Quoniam in Geodæsia periculosissima est mensuratio per angulos tutissima vero per latera hoc unum adhibendo problema : ex datis Trianguli lateribus aream invenire. Hinc operæ pretium mihi visum est modum excogitandi quo Tabula arias ex lateribus facile exhibens calculetur. Et quidem videbatur numeros omnes v. g. usque ad 100 esse ordine con3nandos. Verum quia multæ intercurrunt con3nationes inutiles, ea scilicet, in quibus tertium latus æquile vel maius duobus reliquis simul, hinc interrumpebatur progressio. Ideo ut invenirem progressionem quæ non interrumperetur, sumsi differientias illas sive excessus quibus dua latera excedunt tertium, nempe $a+b-c$ æqu. $f$ ; $a-b+c$ æqu. $e$ ; $-a+b+c$ æqu. $d$ unde fit $a$ æqu. $\frac{e+f}{2}$ et $b$ æqu. $\frac{d+f}{2}$ et $c$ æqu. $\frac{d+e}{2}$. Et area trianguli est $\sqrt{\frac{d}{2}, \frac{e}{2} , \frac{f}{2} , \frac{d+e+f}{2}} \ \textrm{æqu.} \ \frac{\sqrt{\begin{matrix} def & \cap & d \\ &&e \\ &&f \end{matrix}}}{4}$. Ut autem fractiones absint faciemus $d$. $e$. $f$. pares (si faciamus omnes tres impares tunc quidem $a$. $b$. $c$. sont integri, sed non area). Horum parium ergo dimidios nempe $\frac{d}{2}$. $\frac{e}{2}$. $\frac{f}{2}$ sumsimus, id est omnes numeros ordine nam omnium parium dimidii sunt omnes numeri, et horum con3nationes omnes possibiles erunt utiles (expositi in Tabula sub $A$). Cuiuslibet autem con3nationis combinationes dabunt latera Triangulorum omnium in numeris integris possibilium, vel certe eorum dupla. Nam quando latera sunt v.g. $3$.$4$.$6$ tunc $d$.$e$.$f$ sumi deberent impares $1$. $3$. $7$ nam $\frac{1+5}{2}$ æqu. $3$ $\frac{1+7}{2}$ æqu. $4$ $\frac{5+7}{2}$ æqu. $6$. Verum quia in Tabula non reperiuntur $3$. $4$. $6$ sumantur eorum dupla $6$. $8$. $12$ quæ reperietur in Tabula, est area inventa dividatur per $4$ et habebitur area dimidiorum laterum. Sumendo jam ordine omnes numeros positos sub $A$. Voco membra, aggregatum plurium Triangulorum duo latera minora communia habentium v.g. $111$, $112$ etc. item $122$, $123$ etc. At capita voco aggregata plurium membrorum in quibus triangula latus minimum commune habent, ut membra $111$ etc. et $122$ etc. sunt sub uno capite 1. Eodem modo $222$ etc. $233$ etc. sunt sub alio capite 2. Quis sit operandi modus ad fundamentum Tabulæ inveniendum, ejusque varias progressiones pulcherrimas detegendas vide ipsam tabulam et quæ illi ascripsimus. Nunc ostendam tantum quomodo inventa semel progressione, alteris Tabulam calculandam tradere possimus.

Ex his jam habetur modus Tabulam Trangulorum combinandi in infinitum ope Tabulæ membrorum et modus Tabulam membrorum combinandi in infinitum ope Tabulae capitum. Omnia simplici additione. Porro ex terminis seu numeris pro quolibet triangulo ope progressionis inventis extrahatur radix quadratica, et habebitur area Trianguli. Quod ut sine calculo fiat ideo huic Tabulæ adjicienda est Tabula quod valorum extensa circiter usque ad 1 000 000 vel ultra : ita enim facile et satis exacte ex numero quovis utili extrahetur radix adjiciendo aliquot 0 vel zero. Tabula autem quadratorum etiam simplici numerorum imparium additione condi potest. Denique notandum est in quolibet membro Tabulæ Triangulorum non opus esse continuatione, ubi primum pervenitur ad numeros valde inæquales verbi gratia si Trianguli area quæraturque cuius latera $2.31.32$ tale enim triangulum in praxi aut non offeritur, aut non consideratur nam perpendicularis eius a latere parum differt est area ex dimidio eius in basin ductu tuto assumi potest.
Premier feuillet - RECTO -
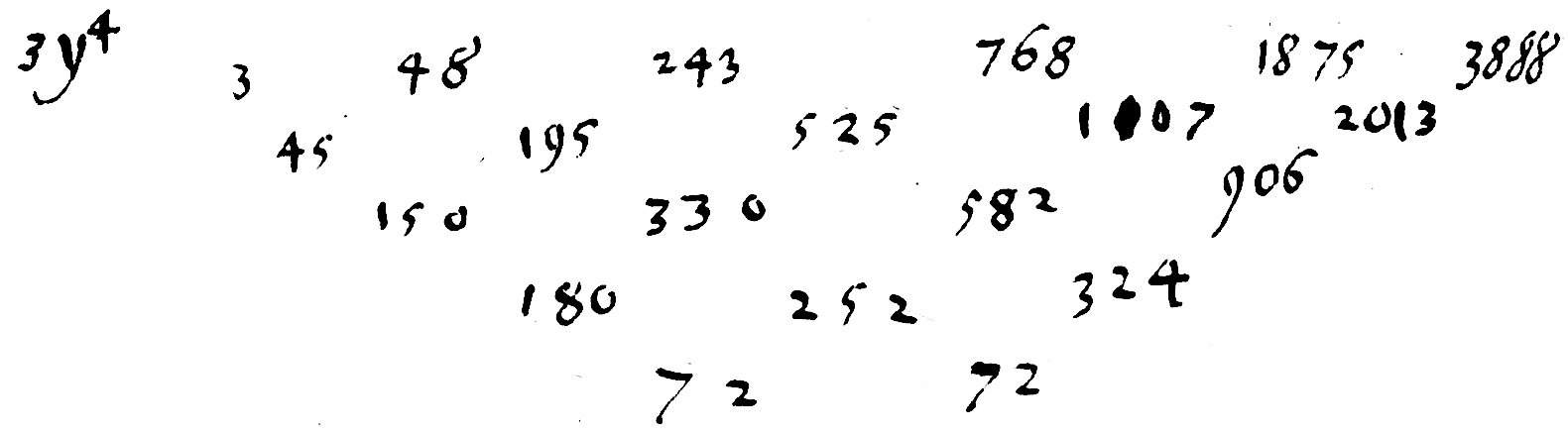
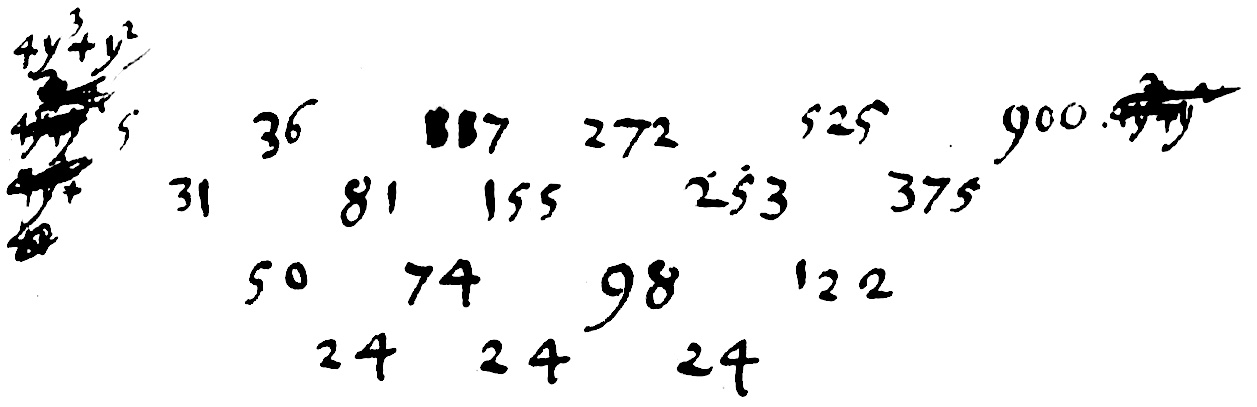
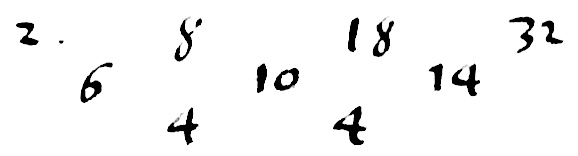
$\begin{array}{ccccc} &&y^3&+&y^2 \\ &&3y&+&1 \\ \hline &&1y^3&&y^2 \\ 3y^4&&3y^3&& \\ \hline 3y^4&+&4y^3&+&1y^2 \end{array}$
$y^2,y+1,,\cap3y+1$ æqu. $3y^4+3y^3+y^3+y^2$ $3y^4+4y^3+y^2$
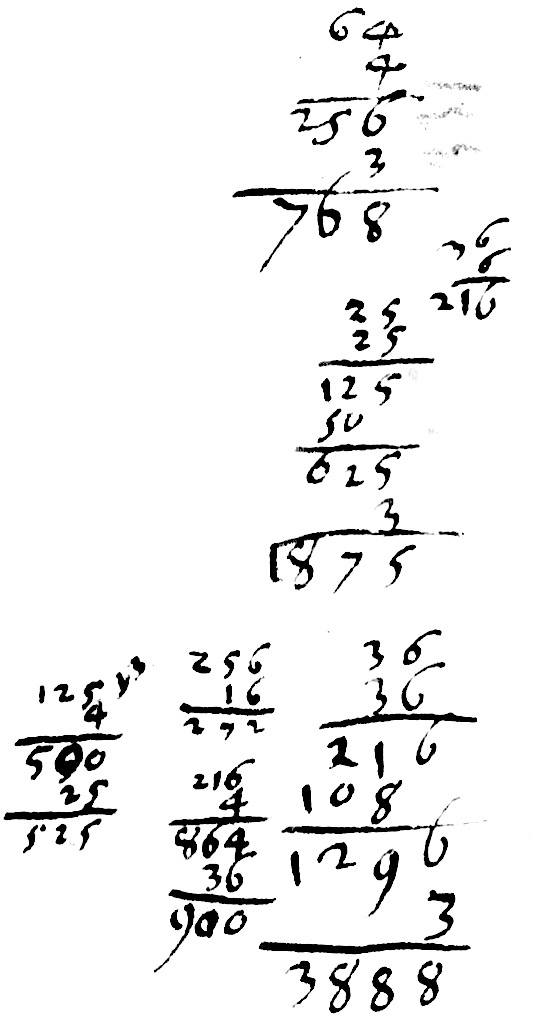
Ea triangula hic non proveniunt in quibus si a summa ductum auferatur tertius restat impar Utile observata, Triangula, in quibus magna ad modum latera duo, et tertium valde parvorum v.g. 2. 21. 22 sunt. Hinc nota uno inutili venientes sequentia inutilia omnia sunt inutilia et omitti possunt
4 5 6
$\begin{array}{ccccc} 4+5&\sqcap&9&& \\ \overline{4+5}&-&6&\sqcap&3 \\ 4+6&-&5&\sqcap&5 \\ 5+6&-&4&\sqcap&7 \end{array}$
- VERSO -
$\begin{array}{cc} 0& \\ 1&1 \\ 3&4 \\ 5&9 \\ 7&16 \\ 9&25 \\ 11&36 \end{array}$
Tabulæ huic addenda est : Tabula quadratorum. Facile est Tabulam hanc quadratorum pariter ac Tabulam potentiarum ab areis invenire per additiones differentiarum ita enim hoc commodum habemus, quod additione ad præcedentia producimus sequentia et ita lucramur neque enim hoc modo quemlibet terminum per se integrum calculare cogamur sed præcedenti labore utimur.
