Translation of Untitled (Tables sur la formule de Heron) [FR]
Folio principal - RECTO -
DE LA FONDATION DE LA TABLE DES AIRES DES TRIANGLES ETANT DONNES LES COTES
Mars 1678
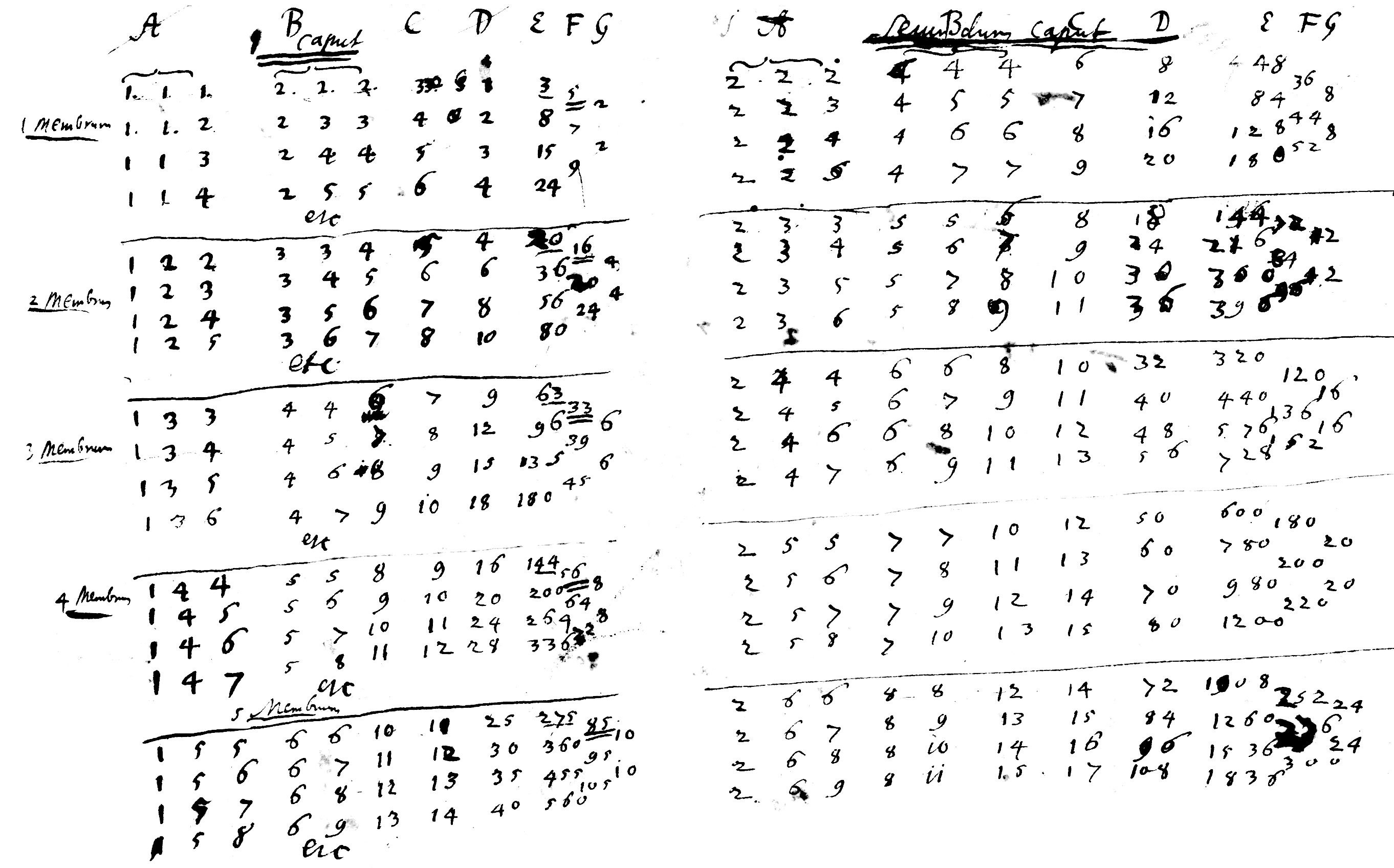

$A$ : les nombres combinés dans l'ordre, c'est-à-dire les excès de deux quelconques des côtés du triangle contenus dans $B$ au dessus du troisième.
$B$ : Les côtés possibles de tous les triangles en nombres, au moyen de certains excès tels que $111$, $122$, $234$ ou $456$. En effet, on dupliquera seulement ceux-ci et on considérera cependant ainsi leurs doubles comme $222$, $244$ ou $468$ de sorte qu'ensuite on divise par $16$ le carré obtenu $E$ de l'aire du triangle, comme $3$, $15$ ou $135$. Le quotient sera le carré de l'aire du triangle cherché.
$C$ : La somme des nombres qui sont sous $A$, c'est-à-dire la demi-somme de ceux contenus dans $B$, ou la demi-somme des côtés du triangles.
$D$ : Le produit de trois nombres $A$ continument multipliés entre eux.
$E$ : Le produit de $C$ par $D$, c'est-à-dire le carré de l'aire du triangle dont les côtes sont $B$, c'est-à-dire que si on extrait la racine carré du nombre $E$, on obtiendra l'aire du triangle.
$F$ : Les différences des carrés des aires, c'est-à-dire des nombres $E$.
$G$ : Les différences des différences, qui seront toujours les mêmes puisque les deux premiers nombres restent identiques.
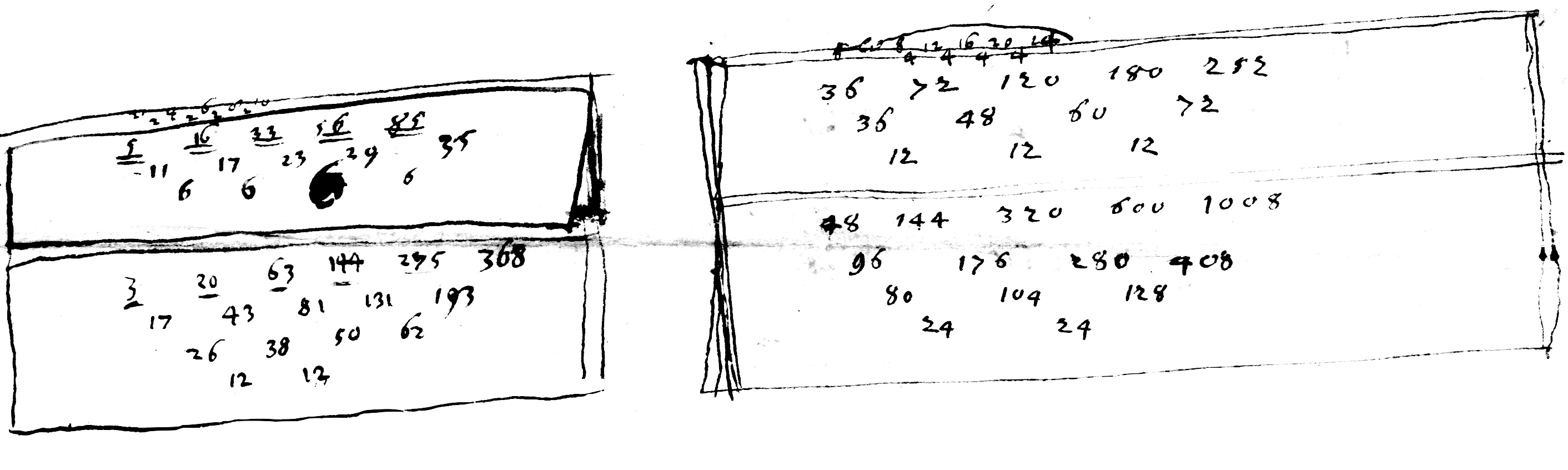
La progression de ces mêmes $G$ et des premiers termes eux-mêmes de $F$ et de $E$ dans n'importe quel membre dans les termes $A$ de la même tête, c'est-à-dire le transport d'un membre vers un membre.
La progression des différences transportées d'un membre vers un membre, est prise d'une tête vers une tête.
$\begin{array}{ccc} 2&6&12 \\ 4&12&24 \\ 6&18&36 \\ 8&24&48 \end{array}$
La progression des premiers de $G$, $E$ et $F$ dans n'importe quelle tête, c'est-à-dire le transport dans les termes $A$ de n'importe quelle tête, ou encore le transport d'une tête vers une tête.
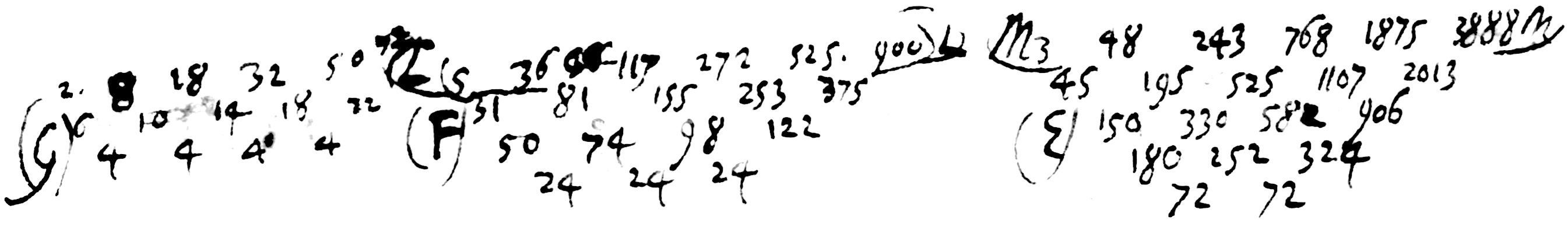
$L = 4y^3+y^2$ étant donné que $y$ est le premier $A$ de la tête. $M=3y^4$
$\begin{array}{c|cccccccc} 1&0&0&0&0&0&0&0&0 \\ 2&0&3&0&1&0&3&0&0 \\ 3&0&4&7&7&1&2&1&3 \\ 6&0&7&7&8&1&5&1&3 \\ \hline &1&5&5&6&3&0&2&6 \end{array}$
$\begin{array}{ccccccccc} 2)&0&7&7&8&1&5&1&3 \end{array}$
La meilleurs voie se trouve par les logarithmes des trois nombres sous $A$ et du quatrième sous $C$. On ajoute les logarithmes l'un après l'autre, et par la moitié prise de la somme, on obtiendra le logarithme de l'aire cherchée. Par exemple, si les côtés du triangle sont $3$, $4$ et $5$, alors les logarithmes des différences $1$, $2$ et $3$ seront :
$\begin{array}{ccccccccc} &0&0&0&0&0&0&0&0 \\ &0&3&0&1&0&3&0&0 \\ &0&4&7&7&1&2&1&3 \\ \hline +&0&7&7&8&1&5&1&3 \end{array}$ $\begin{array}{ccccccccc} &0&7&7&8&1&5&1&3 \\ &&&&&&&&2 \\ \hline +&1&5&5&6&3&0&2&6 \\ -&0&6&0&2&0&6&0&0 \\ \hline &0&9&5&4&2&4&2&6 \end{array}$
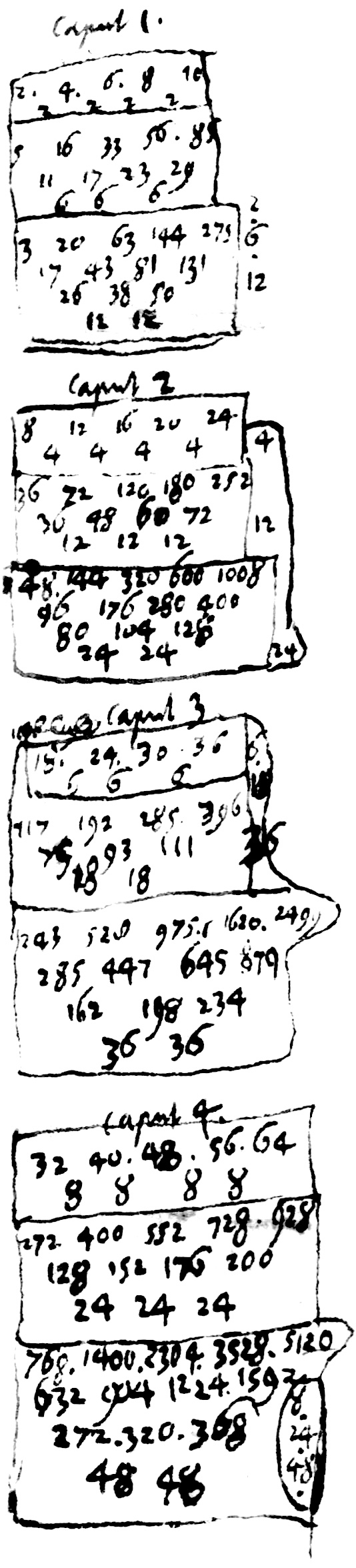
Pour réalise la progression, il faut quatre triangles dans chaque membre, cinq membres dans chaque tête. Et donc six têtes pour le calcul total.
$\fbox{$\begin{array}{ccccccccccccc} 5&6&6&&11&11&12&&17&&180&&3060 \end{array}$}$
$\begin{array}{ccccccccccccc} 6&7&7&&13&13&14&&20&&294&&5880 \end{array}$
- VERSO -
Puisqu’en Géodésie, la mesure par les angles est la plus périlleuse alors que celle par les côtés est bien plus sûre, je vais m’appliquer à ce seul problème : à partir des côtés donnés d’un triangle, trouver l’aire. Il m’a semblé à partir de là qu’il valait la peine qu’on calcule une méthode d’invention, au moyen d’une table qui exhibe facilement les aires à partir des côtés. Et certes, il semblait qu'il faille que tous les nombres, par exemple jusqu’à 100, soient con3nisés en ordre. En réalité, comme il intervient de nombreuses con3naisons inutiles, et ce bien-sûr, lorsque le troisième côté est égal ou plus grand que l’ensemble des deux restants, la progression s’interrompait. Dès lors, pour trouver une progression qui ne s’interrompe pas, j’ai choisi ces différences, c’est-à-dire les excès par lesquels deux côtés surpassent le troisième. A savoir : $a+b-c = f$ ; $a-b+c = e$ ; $-a+b+c = d$ et donc $a = \frac{e+f}{2}$, $b = \frac{d+f}{2}$ et $c = \frac{d+e}{2}$. Et l'aire du triangle vaut : $\sqrt{\frac{d}{2}.\frac{e}{2}.\frac{f}{2}.\frac{d+e+f}{2}} = \frac{\sqrt{\begin{matrix} def & \times & d \\ &&e \\ &&f \end{matrix}}}{4}$ De plus, pour que les fractions disparaissent, nous ferons en sorte que $d$, $e$, $f$ soient pairs (si nous faisions en sorte qu’ils soient tous trois impairs, alors certes $a$, $b$ et $c$ seraient des entiers mais pas l’aire). Ainsi nous choisissons donc les moitiés de ces pairs à savoir $\frac{d}{2}$, $\frac{e}{2}$ et $\frac{f}{2}$, c’est-à-dire tous les nombres dans l’ordre car en effet les moitiés de tous les pairs forment tous les nombres, et toutes leurs con3naisons possibles seront utiles (représentées dans la table sous $A$). De plus les combinaisons de n'importe quelle con3naison donneront les cotés de tous les triangles possibles en nombres entiers ou du moins leurs doubles. En effet, quand les côtés sont par exemple $3$, $4$ et $6$, alors on aurait du choisir pour $d$, $e$ et $f$ les impairs $1$, $3$ et $7$, en effet $\frac{1+5}{2}= 3$, $\frac{1+7}{2}= 4$ et $\frac{5+7}{2} =6$. En vérité, puisqu'on ne trouve pas dans la table $3$, $4$ et $6$, on doit choisir leurs doubles $6$, $8$ et $12$, que l'on trouvera dans la table, et ayant divisé l'aire trouvée par $4$, on obtiendra l'aire des demi-côtés. Il faut encore choisir dans quel ordre on dispose les nombres sous $A$. J'appelle les membres l'ensemble de plusieurs triangles ayant en commun les deux plus petits côtés, par exemple $111$, $112$ etc. mais aussi $122$, $123$, etc. Et j'appelle les têtes les ensembles de plusieurs membres dans lesquels les triangles ont en commun les plus petit côté. Ainsi, les membres $111$, etc. et $122$, etc. sont sous la tête 1. De la même manière, $222$, etc. $233$ etc. sont sous une autre tête, 2. Et ceci doit être la manière de procéder pour trouver le fondement de la table. Et pour découvrir ses diverses progressions magnifiques, voir cette table et ce que nous avons écrit à côté. Maintenant, il faut seulement que je montre comment, ayant trouvé une seule fois la progression, nous pourrons transmettre à d'autres la table à calculer.

A partir de ceux-ci, on obtient déjà le moyen de combiner à l'infini la table des triangles grâce à la table des membres, et le moyen de combiner à l'infini la table des membres grace à la table des têtes. Le tout simplement par l'addition. D'autre part, on extrait la racine carré à partir des termes, ou nombres, trouvés pour n'importe quel triangle à l'aide de la progression, et on obtiendra l'aire du triangle. Ainsi cela se produit sans calcul de sorte qu'on pourrait adjoindre à cette table une table dont les valeurs sont étendues jusqu'à 1 000 000 environ voir plus. Dès lors, en effet, on extraira facilement et de façon suffisamment précise, la racine à partir de n'importe quel nombre utile, en ajoutant un certain nombre de $0$ ou zéros. En outre, on peut également fonder la table des carrés par la simple addition des nombres impairs. Enfin, il faut noter que dans n'importe quel membre de la table des triangles, il n'est pas nécessaire de continuer là où l'on parvient à des nombres vraiment distincts. Par exemple, si l'on cherche l'aire du triangle dont les côtes sont tels : $2.31.32$. En effet, en pratique, un tel triangle, ou bien on ne présente pas, ou bien n'est pris. De fait, sa perpendiculaire ne diffère guère du côté et l'on peut considérer sans crainte l'aire comme sa moitié multipliée par la base.
Premier feuillet - RECTO -
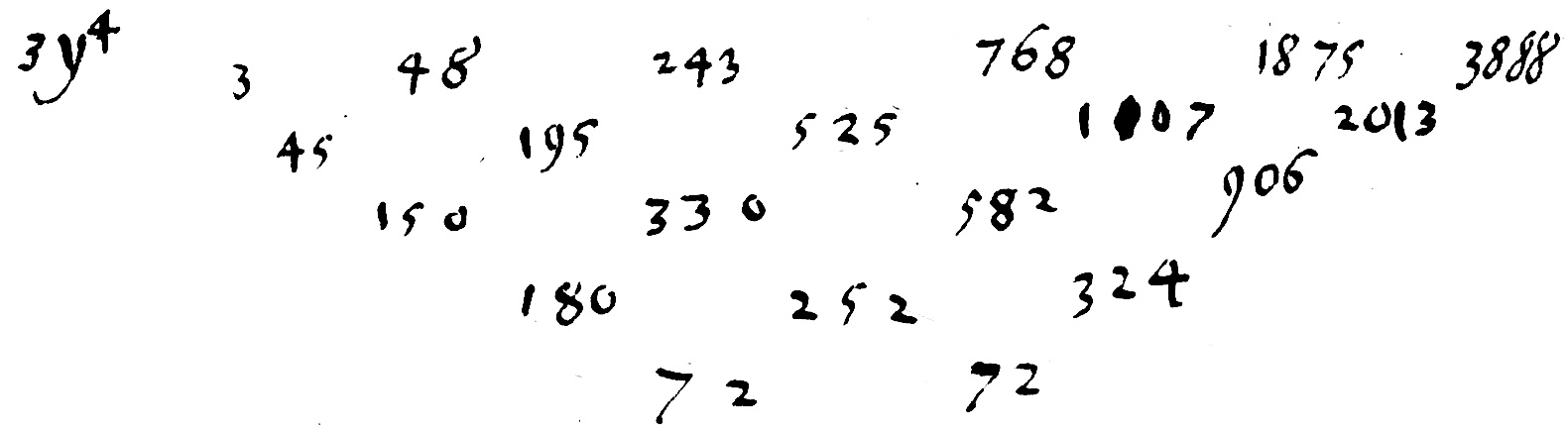
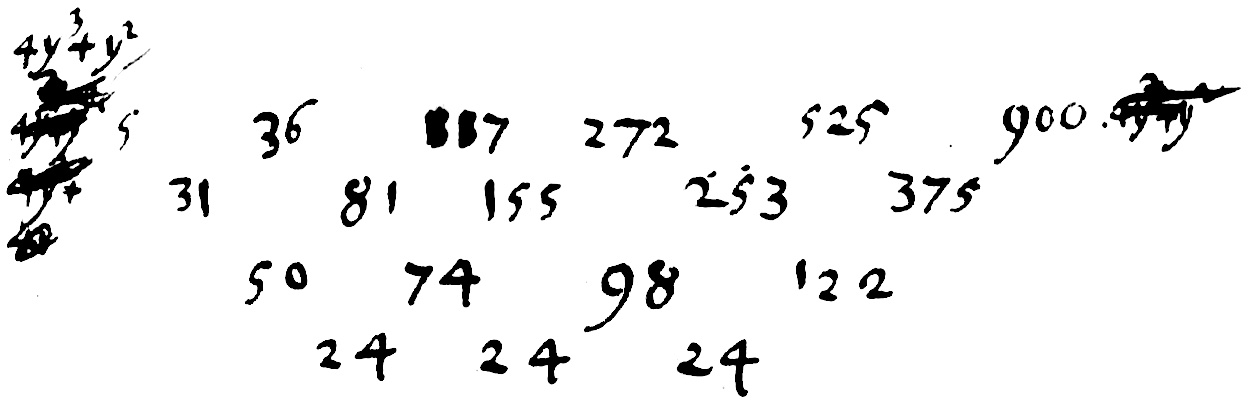

$\begin{array}{ccccc} &&y^3&+&y^2 \\ &&3y&+&1 \\ \hline &&1y^3&&y^2 \\ 3y^4&&3y^3&& \\ \hline 3y^4&+&4y^3&+&1y^2 \end{array}$
$y^2(y+1)\times(3y+1)$ égal $3y^4+3y^3+y^3+y^2$ $3y^4+4y^3+y^2$
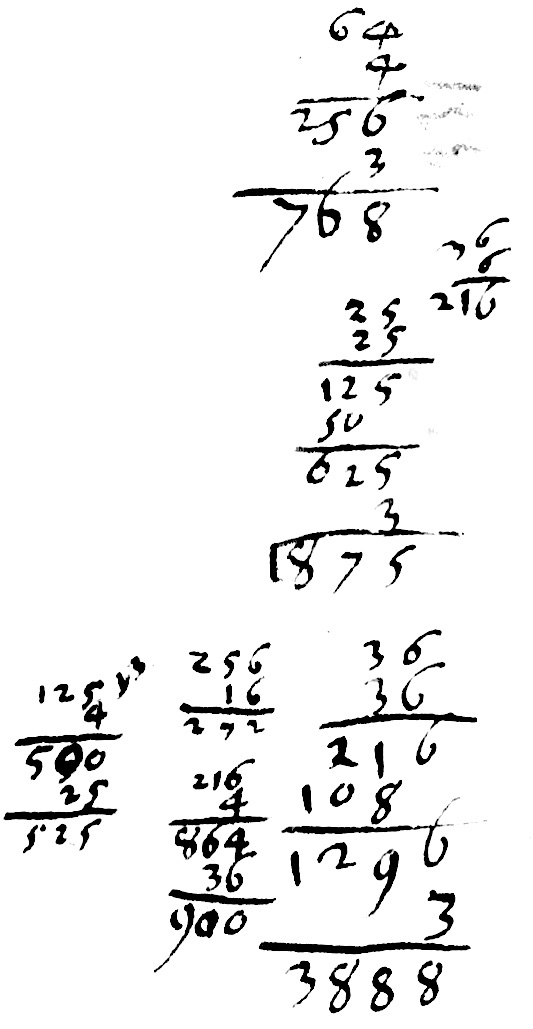
Ces triangles dans lesquels, si on retranche le produit de la somme, le troisième reste impair, ne se produisent pas Il est utile d'observer les triangles dans lesquels les deux cotés sont bien grands et le troisième est de loin des plus petits, comme le sont par exemple 2, 21, 22. A partir de là, on note qu'une fois qu'on est parvenu à des inutiles, tous les suivants sont inutiles et peuvent être omis.
4 5 6
$\begin{array}{ccccc} 4+5&\sqcap&9&& \\ \overline{4+5}&-&6&\sqcap&3 \\ 4+6&-&5&\sqcap&5 \\ 5+6&-&4&\sqcap&7 \end{array}$
- VERSO -
$\begin{array}{cc} 0& \\ 1&1 \\ 3&4 \\ 5&9 \\ 7&16 \\ 9&25 \\ 11&36 \end{array}$
Ce qu'il faut ajouter à cette table : la table des carrés. Il est facile de trouver à partir des aires cette table des carrés, mais aussi de la même manière, la table des puissances, par l'addition des différences. Ainsi, en effet, nous obtenons un moyen commode puisque par l'addition aux précédents nous produisons les suivants et ainsi nous nous ménageons. Et effet, par ce moyen, nous ne sommes pas contraints de calculer chaque terme en entier par lui-même, mais nous nous servons du travail précédent.
