Traduction de Tabula Numerorum Arithmeticae Replicationis seu Figuratorum interpolata
Table interpolée des nombres de replication arithmétique ou figurés.
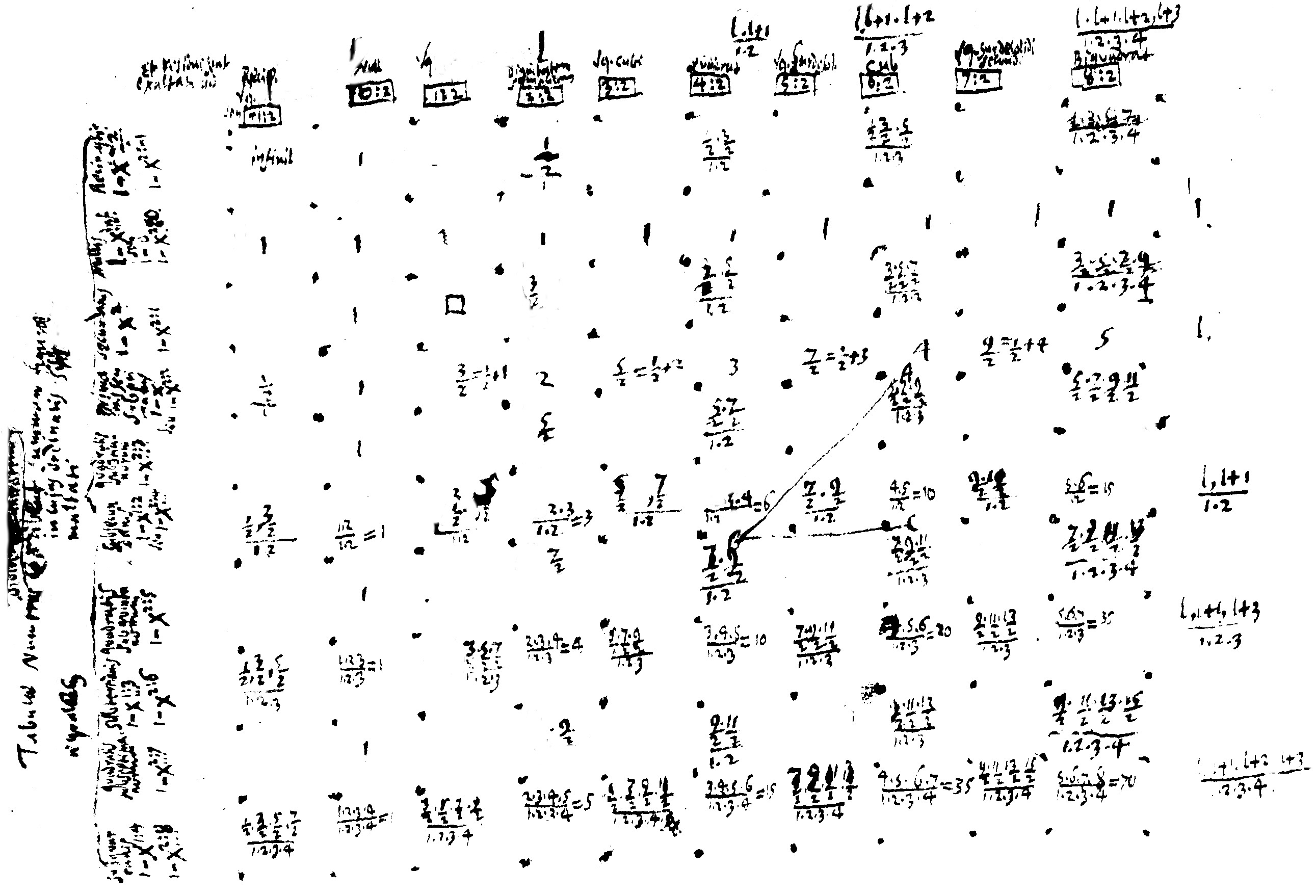
$\int \left(1-x^{\frac{2}{p}}\right)^{n = \frac{m}{2}}dx$ d'où l'on considère que dans $\int \left(x^{\frac{w}{p}}-x^{\frac{w}{p} + \frac{h}{p}}\right)^{n}$, on a $w=0$, $h=2$, $n=\frac{m}{2}$. Et à partir de la règle générale que j'avais trouvée, selon laquelle cette somme vaut, dans le cas de la totalité depuis $x=0$ jusqu'à $x=1$ : $\frac{p.nh.(n-1)h.(n-2)h \dots (n-(n-1))h}{(p+nw+nh)(p+nw+(n-1)h)(p+nw+(n-2)h)(p + nw + (n-3)h)\dots (p+nw+(n-n)h)}$\footnote{\textit{NB} : Pour le dernier facteur du dénominateur de la fraction $\frac{p, nh, (n-1)h, (n-2)h, \ \textrm{etc usque ad} \ (n-(n-1))h}{p+nw+nh, p+nw+(n-1)h, p+nw+(n-2)h, p + nw + (n-3)h, \ \textrm{etc. usque ad} \ (n-n)h}$, Leibniz a écrit "$(n-n)h$" au lieu de "$(p+nw+(n-n)h)$". Nous avons corrigé cela dans la traduction.} \newline soit : \newline - \hfill{$\frac{p. m(m-2)(m-4)(m-6)\dots 2}{(p+m)(p+m-2)(p+m-4)(p + m-6)(p+m-8)\dots (p+0)}$ \hfill{-} Ainsi, on épuise aussi bien le numérateur que le dénominateur si $m$ est pair, c'est-à-dire, si $n$ est un entier. Posons déjà que $p$ est pair, c'est-à-dire divisible par $h$, donc ici $2$ alors une infinité de facteurs dans le numérateur se compensent avec une infinité de facteurs dans le dénominateur. Est-ce qu'ils se compenseront ainsi de sorte que l'infini s'évanouisse ? Voyons par exemple si $p=6$ et $m=1$, alors on a : \newline - \hfill{$\frac{6.1.-1.-3.-5.-7.-9.-11.-1.,-15 \dots}{7.5.3.1.-1.-3.-5.-7.-9.-11.-13.-15 \dots}$} \hfill{-} \newline Est-ce qu'on a donc $= \frac{6}{7.5.3} = \frac{2}{5.7}$ mais la table donne $\frac{1}{\frac{\frac{3}{2}.\frac{5}{2}.\frac{7}{2}}{1.2.3}}=\frac{8.1.2.3}{3.5.7} = \frac{16}{5.7}$. Il semble que $8.2$ (c'est-à-dire $16$) provient du nombre de $h$, c'est-à-dire de $2$, non neutralisés dans le numérateur, autant qu'on compte de nombres dans ce même dénominateur, ce qui peut être montré en rétablissant $h$, c'est-à-dire $2$ : \newline - \hfill{$\frac{6.\frac{1}{2}2.\left(\frac{1}{2}-1\right)2.\left(\frac{1}{2}-2\right)2.\left(\frac{1}{2}-3\right)2.\left(\frac{1}{2}-4\right)2.\left(\frac{1}{2}-5\right)2 \dots}{\left(3+\frac{1}{2}\right)2.\left(2+\frac{1}{2}\right)2.\left(1+\frac{1}{2}\right)2.\left(\frac{1}{2}\right)2. \left(-1+\frac{1}{2}\right)2. \left(-2+\frac{1}{2}\right)2. \left(-3+\frac{1}{2}\right)2\dots}$} \hfill{-} Une autre exemple : soit $p=8$ et $n=\frac{3}{2}$, alors à partir de la règle, on produira : \newline - \hfill{$\frac{8.\frac{3}{2}2.\left(\frac{3}{2}-1\right)2.\left(\frac{3}{2}-2\right)2.\left(\frac{3}{2}-3\right)2.\left(\frac{3}{2}-4\right)2.\left(\frac{3}{2}-5\right)2 \dots}{\left(4+\frac{3}{2}\right)2.\left(3+\frac{3}{2}\right)2.\left(2+\frac{3}{2}\right)2.\left(1+\frac{3}{2}\right)2. \left(\frac{3}{2}\right)2.\left(-1+\frac{3}{2}\right)2.\left(-2+\frac{3}{2}\right)2 \dots} = \frac{8}{11.9.7.5}$} \hfill{-} \newline mais on devrait avoir $\frac{(1.2.3.4).8}{11.9.7.5}$, et ainsi il semble qu'on doit corriger la règle. Construisons la règle à partir de cette table et voyons ensuite s'il est possible de l'unifier aux premières. Soit $\frac{p}{2} = q$, on obtient : $\int\left(1-x^{\frac{1}{q}}\right)^{\frac{m}{2}} = \frac{q.(q-1)(q-2) \dots 1}{\frac{m.2}{2}.\frac{m+2.2}{2}.\frac{m+3.2}{2} \dots \frac{m+(q-1).2}{2}} = \frac{q(q-1)(q-2) \dots (q-(q-1))}{\frac{m+(q-1).2}{2}.\frac{m+(q-2).2}{2} \dots \frac{m+(q-q).2}{2}}$ \footnote{\textit{NB} : Dans le premier facteur du dénominateur de $\frac{q,q-1,q-2, \ \textrm{etc. usque ad} \ 1}{\frac{m+2}{2},\frac{m+2.2}{2}, \frac{m+3.2}{2}, \ \textrm{usque ad} \ \frac{m+(q-1).2}{2}}$, Leibniz a écrit "$\frac{m+2}{2}$" au lieu de "$\frac{m.2}{2}$". Nous avons corrigé cela dans la traduction.} Ainsi, on parvient à la chose si $m$ et $q$ sont des entiers. En revanche si $q$ est fractionnaire $ = \frac{p}{2}$, on y parvient toutefois, à condition que $m$ soit pair. C'est pour cette raison que l'on introduit l'impair lorsqu'on évalue si finalement un infinité de facteurs se neutralisent bel et bien mutuellement. C'est ce qu'il faut faire, et ensuite poursuivre avec $\int\left(1-x^{\frac{1}{q}}\right)^{\frac{m}{3}}$ et $\int\left(x^1-x^{\frac{1}{q}}\right)^{n}$ jusqu'à ce qu'on parvienne à $\int\left(x^w-x^{\frac{1}{q}}\right)^{\frac{m}{r}}$. Et il faut comparer cela avec les premières règles, et regarder pour $(x^w - x^p)^n$ au sein desquels on obtient aussi des interpolations. C'en est de peu que nous n'obtenions enfin une règle vraiment universelle qui unit l'annulation de l'infini pour ce dont on peut déterminer la quadrature de façon absolue, et l'infini lorsque c'est nécessaire. Et qu'elle montre enfin ensemble les connexions transcendantes qu'ont entre eux ce dont on peut faire la quadrature. Dans chaque table, on obtient que diverses sommations se répondent entre elles de façon certaines dans leurs positions, c'est-à-dire que la table est presque dupliquée. On aurait ensuite avancé un pied vers les décompositions des figures, de fait, la dernière n'est pas $1$, mais $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{4}$ $\dots$, ou encore $\frac{1}{2}$, $\frac{1}{4}$ et $\frac{3}{4}$ puis $\frac{1}{8}$,$\frac{3}{8}$, $\frac{5}{8}$ et $\frac{7}{8}$. Est-ce que, maintenant, l'on peut imaginer aussi des règles, qui aient au moins l'air utiles ? Finalement, il faut voir si l'on ne déduit pas ces règles à partir de nos séries infinies et donc qu'on représente une ordonnée irrationnelle par une série rationnelle. Et il en va de même pour la sommation. Mais de plus, on applique celle-ci pour des cas particuliers. Et il faut voir comment l'on déduit de la règle les propriétés que la table représente par induction, comme ici que $A+B = C$
[marge] Toujours deux membres dans $A$ et dans $B$, se dirigeant de façon perpendiculaire et transverse vers le même lieu $C$, par un saut simple. Les sommés composent le membre du lieu $C$, ainsi $A$, $\frac{\frac{5}{2}.\frac{7}{2}.\frac{9}{2}}{1.2.3} + B$, $\frac{\frac{7}{2}.\frac{9}{2}}{1.2}$ donne $C$ c'est-à-dire $\frac{\frac{7}{2}.\frac{9}{2}.\frac{11}{2}}{1.2.3}$
[Noms des colonnes]
- Inverse de $\sqrt{^{}}q$ c'est-à-dire $\fbox{$-1/2$}$
- Nul $\fbox{$0/2$}$
- $\sqrt{^{}}q$ $\fbox{$1/2$}$
- De simples dignités $\fbox{$2/2$}$
- $\sqrt{^{}}q$.du cube $\fbox{$3/2$}$
- Carré $\fbox{$4/2$}$
- $\sqrt{^{}}q$ du sursolide $\fbox{$5/2$}$
- Cube $\fbox{$6:2$}$
- $\sqrt{^{}}q$ du second sursolide $\fbox{$7/2$}$
- Bicarré $\fbox{$8/2$}$
[Noms des lignes]
- sous-quaternaires $1 - x^{1:4}$ $1 - x^{2:8}$
- carrés des sous-septénaires $1 - x^{2:7}$
- sous-tertiaires $1 - x^{\underset{^{.....}}{1:3}}$ $1 - x^{2:6}$
- carrés des sous-quintenaires $1 - x^{2:5}$
- sous-secondaires $1 - x^{1:2}$ seu $1 - x^{\underset{^{.....}}{2:4}}$
- carrés des sous-tertiaires $1 - x^{\underset{^{.....}}{2:3}}$
- primaires ou sous-primaires $1 - x$ seu $1 - x^{2:2}$
- secondaires $1 - x^{2}$ $1 - x^{2:1}$
- nuls $1 - x^{\underset{^{.....}}{\textrm{inf.}}}$ seu $1-0$ $1 - x^{2:0}$
- inverses des carrés $1 - x^{\underset{^{...}}{-2}}$ $1 - x^{2:-1}$
[Titre de la table]
Les nombres de la table, en divisant l'unité, expriment la somme de la figure dans les ordonnées de laquelle les mutliplications sont égales à :
[Note dans le coin supérieur gauche de la table]
Et les restes sont élevés à :
