Traduction de Sans titre, sur l’interpolation de Mengoli
- Recto -
20 mars 1679


L'emploi de Newton, par cette progression, donne seulement, extraits de la table ♀︎ : $\sqrt{1}$, $\sqrt{ar}$, $\sqrt{a^2r^2}$, $\sqrt{a^3r^3}$, $\dots$. Et de celles-ci, il a fait des interpolations et des démonstrations par et pour la quadrature, au moyen des séries infinies. Et il faut traiter dans celles-ci les séries déjà choisies et les autres. Ces tables montrent en revanche où les quadratures dépendent de la quadrature du cercle, ce que ne montrent pas les séries.
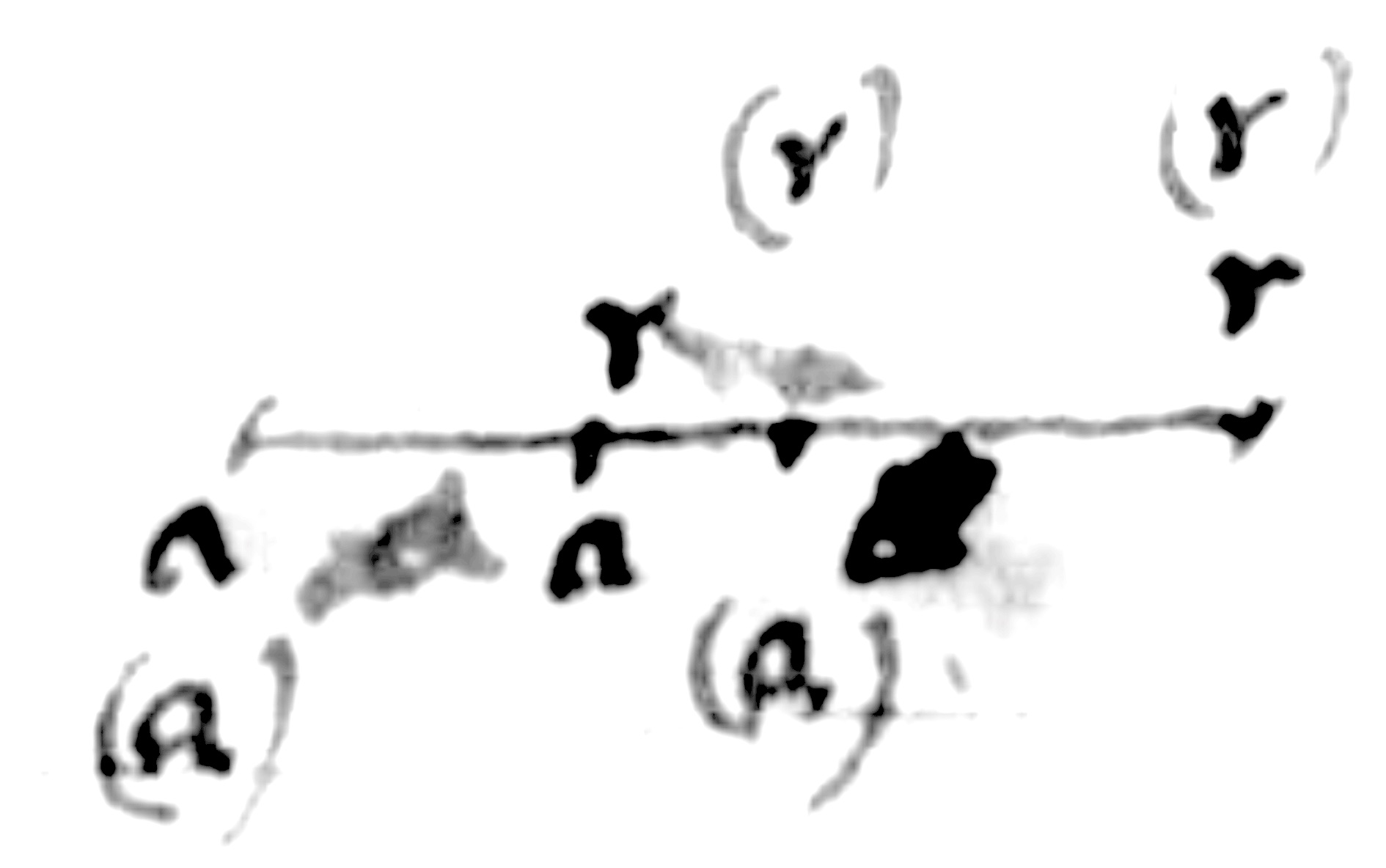
$AB=a$
$BC=r$

$\sqrt[2]{a^zr^\nu}=BD$ Si aussi bien $z$ que $\nu$ sont des nombres impairs, alors la figure dont on a ici l'ordonnée dépend de la quadrature du cercle, autrement elle quadrable de façon absolue.
$BD = \sqrt{ar}$, en supposant que $BDQ$ est un quadrant de cercle. $AC=CQ$
La table ♀︎ est celle des figures dont on doit faire la quadrature.
............... ☽ ... des nombres qui expriment ces quadratures.
Dans la table ☽, on peut ajuster les séries des fractions de l'unité aux termes de sorte qu'ils s'apparient là où ils semblaient discordants. Ainsi pour $AB$, on peut écrire $\frac{2}{2}$, $\frac{2}{3}$, $\frac{2}{4}$, $\frac{2}{5}$, $\dots$ ; pour $BC$, on peut écrire $\frac{6}{15}$, $\frac{4}{15}$, $\frac{4}{15}$, $\frac{6}{15}$ et pour $DE$ on peut écrire : $\frac{4}{8}$, $\frac{4}{15}$, $\frac{4}{24}$, $\frac{4}{35}$, $\frac{4}{48}$, $\frac{4}{63}$, $\frac{4}{80}$. Ici, il apparait que le terme $D$ peut et doit être exprimé de plusieurs manière, afin qu'il s'accorde avec les diverses séries. Ainsi pour la série $AB$, on l'exprime par $\frac{2}{4}$ et pour la série $DE$ par $\frac{4}{8}$. Si l'on donne une certaine expression commune à tous les termes dans ☽, opérant les quadratures partout dans la table ☽. A partir des termes correspondants dans la table ♀︎ (dont on fait les quadratures partout), on dérivera une règle constante sur les exposants et on obtiendrait la valeur de celui-ci : $b$. Et puisqu'il est transcendant et qu'il s'intègre à la mesure du cercle, il faut chercher cette expression commune dans les termes transcendants.
On peut déterminer de manière générale les termes de la table ☽ à partir des termes de la table ♀︎ en appliquant les séries infinies. Mais on souhaite que, à la place de la série, la chose se réduise à une puissance ou une racine dont l'exposant n'est pas un nombre rationnel. En outre, il faut examiner si par quelque moyen l'on pourrait trouver la quadratrice de celles-ci : $\sqrt{ar^2}$, $\sqrt{ar^4}$ grâce au calcul différentiel et aussi si l'on pourrait trouver la quadratrice de celle-ci $\sqrt{ar}$. Il est possible que les exposants de cette quadratrice deviennent irrationnels là où l'on doit faire en sorte que, d'aventure, ces irrationnelles s'affectent mutuellement entre elles l'une multipliant ou divisant l'autre dans l'exposant de la quadrature, à savoir de celle-ci $\sqrt{ar}$.
[Passage barré]
Soit $z=\frac{1}{y}$, on obtient [coupe] On a de plus $d\left(\frac{1}{y}\right)=\frac{+dy}{y^2}$. Donc $\int$ [coupe]
Il faut examiner $\int z^{d\overline{z}}$ [coupe]
$d\left(\sqrt{z}\right)= \frac{1}{\sqrt{z}}dz$
$d\left(\frac{1}{\sqrt{y}}\right)=\sqrt{y }d\left(\frac{1}{y}\right)$
$\frac{1}{y} - \frac{1}{y+dy} =$ [coupe]
- Verso -
[marge] Note : la table progresse quelques soient $a$ ou $r$, du moment que $da = +dr$, et se poursuit de la sorte à l’infini.
$da = dr$ $dar = da.r + dr.a$.
On a $\int\sqrt[z]{ar} d(ar) = \frac{(ar)^{\left(\frac{1}{z} + 1\right)}}{\frac{1}{z} + 1}$ ou $\frac{\sqrt[{}^{\frac{z}{1+z}}]{ar}}{\frac{1+z}{z}}$[1] $= \int r\sqrt[z]{ar}da + \int a\sqrt[z]{ar}dr$
De là, il apparait que la quadrature d’une figure de ce genre est donnée par $\int r\sqrt[z]{ar}da$, en posant $dr=da$. Mais celle-ci : $\int a\sqrt[z]{ar}dr$ est donnée à partir de la quadrature du cercle, en posant $da=-dr$, et à partir de la quadrature de l’hyperbole, en posant $da=dr$, dans le cas où $\nu$ est une nombre rompu. En effet, s’il s’agit d’un entier alors la quadrature est donnée de façon classique, du moment que $a$ et $r$ sont des quantités rationnelles. NB : $z$ doit être un nombre pair. De façon générale, à chaque fois qu’on se donne la quadrature d’une certaine figure à partir de $a$ et de $r$, en posant $dr=\pm da$, on ajoute à celle-ci une autre semblable, composée à partir de $a$ et de $r$ de la même manière que la première à partir de $r$ et de $a$, comme le montre le calcul. On cherche si l’on peut trouver la sommatrice de celle-ci. Ou alors, si on n’ajoute pas une qui est composée de la même manière, alors on y ajoute une autre dont on donne également la quadrature par une composée de $a$ et de $r$. Il y a de grands abrégés dans ces calculs de quadratures. Il faut voir comment de cette manière l’on montre par le calcul que tous ceux-là dépendent seulement de cela : $\int \overline{\sqrt{ar}d\overline{a}} + \int \overline{\sqrt{ar}d\overline{r}}$
Note : il faut que nous cherchions ces figures de la table qui ont une quadrature absolue et que nous exprimions aussi la quadratrice par $ar$.
Note : $a^2$ ou $a^3$ peuvent également être exprimée par $ar$, en effet, on a $a^2r^0$ ou $a^3r^0$. Donc nous étudierons facilement les quadratrices par la méthode que nous avons déjà notée. Mais une fois que nous aurons les quadratrices, alors par le calcul différentiel, nous dériverons à partir d’elles les termes de la table ♀︎. Et nous verrons s’il est possible de découvrir une certain exposant ou un moyen de calcul ou quelque chose de similaire et d’où il suivrait que tout ceux qui n’ont pas de quadrature exacte se réduisent à un seul $b$. De fait, il faut que nous posions que $b$ est le maximum de la quadrature du cercle $\int \overline{\sqrt{ar}d\overline{a}}$ parmi les choses à calculer, c’est-à-dire qu’on dérivera $\int \sqrt{ar}da$ facilement d’ailleurs. Par exemple $\int r\sqrt{ar}da$ est la quadratrice de cette figure : $\int \left(\sqrt{ar}da\right)dr + \sqrt{ar}da.r.dr$, en posant $da=dr$

$AB=a=\theta D$
$CB=r=\theta E$
$BF=a\sqrt[z]{ar}$
$BG=r\sqrt[z]{ar}$
On donne l'aire $AHGFA$ et de plus on donne l'aire $FGKLF$, en posant donc $FG=KL$ et dès lors $ML=BG$ et $BF = KM$. On aura alors l'aire $FBMLF$ qui est la moitié de celle-ci $FGKLF$, puisque le point $N$ (milieu entre $A$ et $C$) est à égale distance de $B$ et de $M$. Mais puisque $N$ n'est pas un point déterminé, étant donné qu'on peut considérer une autre longueur pour $AC$, il semble qu'on puisse poursuivre ainsi pour les autres. De même, cela suffit par cette méthode pour trouver la série sommatrice pour n'importe quelle partie de ce genre, et l'on obtiendra donc la ligne de la série sommatrice. Et donc pour la totalité. Il faut seulement voir si, par quelque moyen, on aurait pu dériver l'aire $FBMLF$ par le calcul et sans examiner la figure ni à l'aide de l'imagination.
[1] le dénominateur $\frac{1}{z} +1$ est réécrit par Leibniz sous la forme $\frac{z}{z+1}$ au lieu de $\frac{z+1}{z}$. Nous avons corrigé cela dans la traduction. ↩
