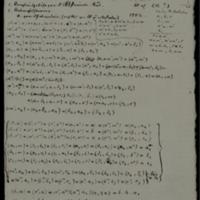Votre recherche dans le corpus : 21 résultats dans 144 notices du site.
Trier par :
La notation gagne(?) quand on remplace c'' par d', c2par d1
Collection : Cod. Ms. Dedekind X 9
Auteurs : Dedekind, Richard
Résultat sur un cas de deux groupes de modules en correspondance
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Tableau théorie des 3 modules de type idéal
Collection : Cod. Ms. Dedekind III 14
Auteurs : Dedekind, Richard
Calculs et tableaux pour n=4 (1897)
Collection : Cod. Ms. Dedekind III 14
Auteurs : Dedekind, Richard
Tableau 3 modules et calculs nombres de classes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Trois modules, tableaux et diagrammes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Chaînes et nombres de classes, symétrie
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Trois modules, calculs et diagrammes 1
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Quelques théorèmes sur les Modul-Gruppen.
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard