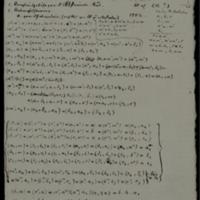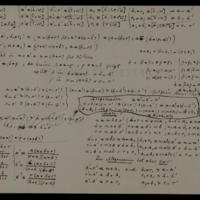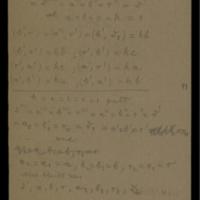Votre recherche dans le corpus : 144 résultats dans 144 notices du site.
Trier par :
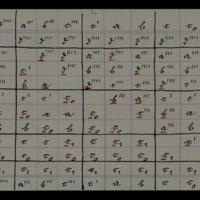
Trois modules, tableaux et diagrammes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Tableau 3 modules et calculs nombres de classes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Propriétés des opérations, modules et idéaux
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs nombres de classes, normes de modules
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs sur des modules finis + Théorème général
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs sur modules finis et idéaux
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Meilleure présentation pour 3 modules a, b, c
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Meilleure présentation pour 3 modules, tableau
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Théorie des trois modules (tableau OX)
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
[Étude d'un groupe] de type module
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Première rédaction de l'article de 1900
Collection : Cod. Ms. Dedekind X 11-2
Auteurs : Dedekind, Richard
Groupe des 28 modules généré par les trois modules a, b, c
Collection : Cod. Ms. Dedekind X 11-2
Auteurs : Dedekind, Richard
Dualgruppe engendré par a, b, c avec Modulgesetz
Collection : Cod. Ms. Dedekind X 11-2
Auteurs : Dedekind, Richard
Petit tableau sans titre
Collection : Cod. Ms. Dedekind X 11-2
Einfache Modulgruppe (oder Kette)
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Tableau pour quatre modules 1, 2, 3, 4
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Courts calculs sur la divisibilité des modules
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Résultat sur un cas de deux groupes de modules en correspondance
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Tableau des Nächste Vielfache et Nächste Theiler
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Recherches autour des nombres de classes
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Formation d'un groupe généré par trois modules quelconques
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard