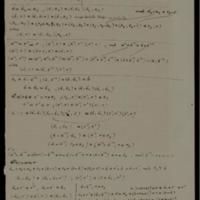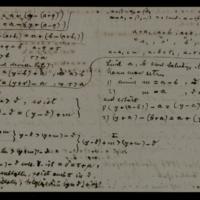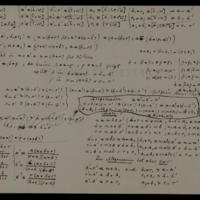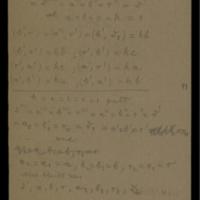Votre recherche dans le corpus : 40 résultats dans 144 notices du site.
Trier par :
Parallélisme entre modules et groupes abéliens
Collection : Cod. Ms. Dedekind X 9
Auteurs : Dedekind, Richard
Sur le dualisme dans la théorie des modules
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard
Quelques théorèmes sur les Modul-Gruppen.
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard
Dualité dans la théorie des modules entre ppcm et pgcd.
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard
Théorie des modules (peut-être : Théorèmes généraux sur les modules, ordres et congruences)
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard
Exemple le plus simple d'un système S qui n'est pas modulaire
Collection : Cod. Ms. Dedekind XI 1
Auteurs : Dedekind, Richard
Calculs sur les modules finis et divisibilité.
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs sur les modules et nombres de classes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Tableau + symétrie en fonction de a, b, c.
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Trois modules, calculs et diagrammes 1
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Chaînes et nombres de classes, symétrie
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Trois modules, tableaux et diagrammes
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Propriétés des opérations, modules et idéaux
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs nombres de classes, normes de modules
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Calculs sur des modules finis + Théorème général
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Meilleure présentation pour 3 modules a, b, c
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Théorie des trois modules (tableau OX)
Collection : Cod. Ms. Dedekind X 11-1
Auteurs : Dedekind, Richard
Dualgruppe engendré par a, b, c avec Modulgesetz
Collection : Cod. Ms. Dedekind X 11-2
Auteurs : Dedekind, Richard
Courts calculs sur la divisibilité des modules
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
La divisibilité d'un module m par un module n sera complètement exprimée par chacune de ces 3 égalités
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Divisibilité, dualité et modules finis
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Théorèmes de théorie des modules avec notation générale
Collection : Cod. Ms. Dedekind X 11-2
Auteurs : Dedekind, Richard
27 octobre 1890, théorème nombre de classes.
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Calculs sur les modules finis et un peu de Modulgesetz
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Relation d'ordre pour modules (tableau)
Collection : Cod. Ms. Dedekind X 10
Auteurs : Dedekind, Richard
Tableau théorie des 3 modules de type idéal
Collection : Cod. Ms. Dedekind III 14
Auteurs : Dedekind, Richard