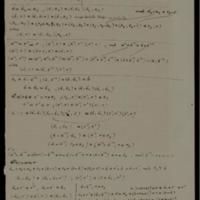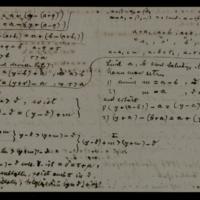Votre recherche dans le corpus : 144 résultats dans 144 notices du site.
Trier par :
Dualgruppe (ohne Modulgesetz) aus a, b, c under der speciellen Annahme : b-c=c-a=a-b
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Über den Dualismus in den Gesetzen der Zahlen-Moduln
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
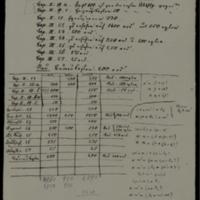
Tableau comparant les modules et les groupes (Frobenius & Stickelberger)
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Calculs sans titre, modules et nombres
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Etude d'une équation avec modules, reposant sur la théorie des trois modules
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Calculs, modules finis et Modulgruppen 1
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Tableaux groupes. Distances entre modules
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Parallélisme entre modules et groupes abéliens
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Différentielles d'un système de modules
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Théorie des trois modules, divisibilité.
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Sur la théorie des Modul-Gruppen (aussi groupes abéliens)
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Calculs sur des modules et nombres de classes
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
La notation gagne(?) quand on remplace c'' par d', c2par d1
Collection : Cod. Ms. Dedekind X 9
Auteur : Dedekind, Richard
Sur le dualisme dans la théorie des modules
Collection : Cod. Ms. Dedekind XI 1
Auteur : Dedekind, Richard
Quelques théorèmes sur les Modul-Gruppen.
Collection : Cod. Ms. Dedekind XI 1
Auteur : Dedekind, Richard
Dualité dans la théorie des modules entre ppcm et pgcd.
Collection : Cod. Ms. Dedekind XI 1
Auteur : Dedekind, Richard
Théorie des modules (peut-être : Théorèmes généraux sur les modules, ordres et congruences)
Collection : Cod. Ms. Dedekind XI 1
Auteur : Dedekind, Richard
Exemple le plus simple d'un système S qui n'est pas modulaire
Collection : Cod. Ms. Dedekind XI 1
Auteur : Dedekind, Richard
Calculs sur les modules finis et divisibilité.
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Calculs sur les modules et nombres de classes
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Trois modules a, b, c (liste, notation3)
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Tableau + symétrie en fonction de a, b, c.
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Trois modules, calculs et diagrammes 1
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard
Chaînes et nombres de classes, symétrie
Collection : Cod. Ms. Dedekind X 11-1
Auteur : Dedekind, Richard